Up: Class 13, Math 696
Next: Homework
Previous: Goals

Reminders

Taking stock

To travel hopefully is a better thing than to arrive, and the true success is to labour. ---Robert Louis Stevenson

We have come to the end of our semester's journey together, and I hope you have found the trip worthwhile. I have enjoyed it.

When I was beginning to design this course, some of my colleagues asked what skills I expected the students to have by the end of the semester. I told them that at a bare minimum, the students would be able to typeset a calculus quiz in LaTeX, verify the solutions with Maple, and give a coherent verbal presentation of the solutions. As the course has developed, we have gone far beyond these minimal competencies.

I hope and believe that your accomplishments this semester include the following.

I would like to have your feedback on the course. Your reactions will help me in making revisions for next year. The one required activity for tonight is to fill out the course evaluation form.

Activities for Class 13

Feedback

The first activity today is to type in LaTeX and print out your comments about the course. I would appreciate feedback about what you liked about the course and what you did not like; what I should keep the same and what I should change in the future.

Your comments are anonymous, and I will not see them until after grades are turned in, so please say what you think. After you print out your comments, give the hard copy to the student who has volunteered to turn in the evaluations to room 623 Blocker.

You can use your Web browser to grab a template for comments.

Brief demonstration of Maple V Release 4

The version of Maple that we have been using under UNIX is Maple V Release 3. The new Release 4 is already available on the PCs in the university PC computer labs (such as the ACC, Blocker 133, where you have been picking up printouts during class). A UNIX version of Release 4 should be installed on the mathematics department systems by the beginning of the spring semester.

I will give a short demonstration of the new Release 4. The primary difference from Release 3 is that the new release of Maple V has a redesigned worksheet interface that supports formatted characters and paragraphs, mathematical expressions inside paragraphs, structured sections, and embedded graphs.

Some of you have experimented with the ``Export as LaTeX'' feature of Maple V. This feature has serious limitations under Release 3 (which is a reason that I have not discussed the feature before). Under Release 4 of Maple V, the ``Export as LaTeX'' feature works much better. It even captures graphs automatically.

More on LaTeX

Slides

We have had occasion to use only the article and letter document classes in LaTeX. There are also report and book document classes, which are good for very long documents.

Here is an example of how to use the slides document class, which is useful for producing transparencies for the overhead projector.

\documentclass{slides}
\begin{document}
\begin{slide}
  \begin{center}
      A sample slide
  \end{center}
  \begin{itemize}
  \item Slides automatically come out in a large font.
  \item This font is expressly designed to be legible when
      displayed via the overhead projector.
  \item Avoid overloading the audience: 
    do not put too many lines on one slide.
  \end{itemize}
\end{slide}
\end{document}

Here are some warnings about using slides for a lecture:

LaTeX2HTML

You have no doubt noticed that LaTeX and HTML share the philosophy of logical design (as opposed to visual design). In both languages you specify structural units, such as sections and paragraphs; choices about font sizes and styles are not supposed to be your primary concern. Because of this similarity, you might imagine trying to build an automated converter from LaTeX to HTML. A fairly good converter called LaTeX2HTML exists for UNIX systems. It is installed on the calclab machines and on the main mathematics server. The command latex2html -h gives some terse help on the syntax, and a complete manual is available.

LaTeX2HTML attempts to translate LaTeX section and list commands into their HTML counterparts. LaTeX2HTML handles mathematical expressions by turning them into gif graphics and automatically linking the graphics into the HTML document. Unfortunately, LaTeX2HTML is not yet smart enough to handle complicated LaTeX documents that use add-on packages such as amsmath. Nonetheless, it does a good job of converting basic LaTeX files.

For an example of a Web page produced from a LaTeX file by LaTeX2HTML, take a look at Sufficient Conditions for Multiply Constrained Extrema by Thomas I. Vogel.

Hodgepodge

Spell checking

It is a pity that Chawcer, who had geneyus, was so unedicated. He's the wuss speller I know of. ---Charles Farrar Browne, Artemus Ward in London

The above quotation is facetious, but nonetheless, people may not take you seriously if your writing contains egregious spelling errors. Many text editors and word processors come with spelling checkers. The editor emacs has an interactive spell checker ispell that is smart enough to skip over most LaTeX control sequences.

The UNIX operating system has a noninteractive spell checker that you can call from the command prompt in a terminal window via spell filename. There is a spelling checker on the Web that will check the spelling in your HTML documents.

However, using a spelling checker does not absolve you of the responsibility of proofreading what you write, as the following poem illustrates. (The poem circulated around the Internet a while back---author unknown.)

I have a spelling checker,
It came with my PC;
It plainly marks four my revue
Mistakes I cannot sea.
I've run this poem threw it,
I'm sure your please too no,
Its letter perfect in it's weigh,
My checker tolled me sew.

(The joke is that the poem has 13 errors, none detectable by the computer program.)

Part of scholarly writing is to verify the references, give proper credit, and spell the names correctly. There is a supposedly authoritative book on Fourier series produced a few years ago by a distinguished publishing house, and I refuse to buy the book because the author consistently refers to ``Gibb's phenomenon.'' I have no confidence in the mathematics of an author who is not careful enough to realize that the man's name is Gibbs, so the overshoot in the Fourier series of a jump function is properly ``Gibbs's phenomenon.''

With such examples in mind, my father once wrote the following verses, titled ``Spelling Lesson.''

Weep for the mathematicians
Posterity acclaims:
Although we know their theorems
We cannot spell their names.

Forget the rules you thought you knew---
Henri Lebesgue has got no Q.

Although it almost rhymes with Birkhoff,
Two H's grace the name of Kirchhoff.

The Schwarz of inequality
And lemma too, he has no T.

The ``distribution'' Schwartz, you see
Is French, and so he has a T.

In Turing's name---no German, he---
An umlaut we should never see.

Hermann Grassmann---please try to
Spell both his names with 2 N's too.

If you should ever have to quote
A Harvard Peirce, be sure to note
He has the E before the I;
And so does Klein. Rules still apply
To Wiener: I precedes the E;
The same for Riemann, as you see.
But Weierstrass, you must agree,
Has it both ways, with EIE.

Fejér, Turán, Cesàro, Fréchet---
Let's make the accents go that way;
Don't lose the squiggly little bits;
They don't mark stress---they're diacrits.

And as for (Radon)-Nikodým,
Restore the accent, that's my dream.

But there is one I leave to you,
Whatever you may choose to do:
Put letters in or leave them out,
Garnish with accents round about,
Finish the name with -eff or -off:
There is no way to spell 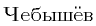Cyrillic Chebyshev.

(For a curious tale about the name given in Cyrillic characters at the end of the poem, see Philip J. Davis, The Thread: A Mathematical Yarn, Birkhäuser, 1983; call number PN6162.D376 1983.)

The writer who neglects punctuation, or mispunctuates, is liable to be misunderstood .... For the want of merely a comma, it often occurs that an axiom appears a paradox, or that a sarcasm is converted into a sermonoid. ---Edgar Allan Poe

PH

Texas A&M University keeps track of your name, telephone number, e-mail address, and so forth in an on-line phone book database named PH. It has a Web interface. You may like to look yourself up and add your URL to the database. (Follow the online instructions.)

Fun and games

There are some nifty games out there in cyberspace that interact with you. For example, did you know that the letters in ``Texas A&M University'' can be rearranged to form ``anxieties must vary'' or ``extra massive unity''? The letters in my name, Harold Philip Boas, can be rearranged to form ``Abolish hippo lard!'' Yahoo has a list of WWW based anagram servers. You might like to find anagrams for your own name.

The Mathematical Quotations Server features the following quotation this week.

Life is good for only two things, discovering mathematics and teaching mathematics. ---Siméon Poisson

Perhaps you would like to test your knowledge against the Pi Trivia Game, or read about the Erdös Number Project, or play Nim against a computer, or look at some classic mathematical puzzles.

Copyright

It used to be that a work had to bear a copyright notice to be protected under United States copyright law. Currently, protection inheres automatically in a textual, graphic, audio-visual, or architectural work once it is ``fixed in a tangible form.'' Consequently, just because you can grab something off the Web does not mean that it is in the public domain. In principle, you should request permission from the work's creator before you use it. Check out the Copyright Website for further information.

Introduction to MATLAB

We have been using Maple to do mathematics on the computer, but there are a number of competing programs. Two main reasons for concentrating on Maple in this course are that Maple is widely available on the the Texas A&M University campus and that Maple is powerful.

The best known competitor to Maple is Mathematica, which has just been released in a new version 3.0. Unfortunately, Mathematica is not widely available on campus; however, version 2.2 is available on the mathematics department's machine fourier.

The program MATLAB (which stands for MATrix LABoratory) is another tool for numerical and graphical analysis. It is available on both the calclab machines and the main mathematics server. Here is a brief introduction to MATLAB.

Open a terminal window and start the program by typing matlab. You should get a command prompt something like >>. Try typing 2+3 and pressing Return to see how MATLAB does simple computations. Notice that, unlike Maple, MATLAB requires no punctuation character to terminate the command (indeed, MATLAB uses a semicolon as a signal to suppress the output!) MATLAB knows all standard functions. Try sqrt(exp(cos(log(2*pi/3)))) for example; you should get the answer 1.4470.

There is built-in help. Typing just help gives a list of help topics. For example, there is a topic matlab/elfun, and typing help matlab/elfun gives a list of elementary functions known to MATLAB. By typing help acot, you can confirm that acot is the inverse cotangent function. There is also a command lookfor that does a (slow) keyword search of the help files.

Now suppose you want to make a plot. Since MATLAB is numerically oriented, you have to feed it a list of numbers (rather than the name of a function). For example, you could say x=[0, 0.2, 0.4, 0.6, 0.8, 1] and then y=cos(x) and then plot(x,y). This creates a rough plot of the cosine function on the interval from 0 to 1. The plot should pop up in a separate window.

Maybe you really wanted a plot of the cosine function on the interval from 0 to Pi. Try x=x*pi and y=cos(x) and plot(x,y). Notice that MATLAB displays the new plot in the same window as before, discarding the previous plot. The plot window stays up until you issue the command close.

The plots above are crude because they use a small number of data points. Try x=linspace(0,pi,101); to define x to be a linearly spaced partition of the interval (0,Pi) into 100 subintervals, and then y=cos(x); and plot(x,y) to get a smoother plot. Try z=sin(x); and plot(x,y,x,z) to plot two functions on the same graph. What does plot(y,x) do?

You can make the graph fancy in various ways. Try some of the following.

The command grid toggles grid lines on and off. The commands axis off and axis on toggle the axes. You can put labels on the plot via xlabel('this labels the x axis') and ylabel('this labels the y axis') and title('this is a title'). You can also place text on the plot interactively by issuing the command gtext('some text'), moving the mouse to the appropriate spot in the plot window, and clicking the mouse.

If you set zoom on, you can expand or contract the plot with mouse clicks.

MATLAB deals well with arrays and matrices. If you set a=[1,2,3,4] and b=[5,7,11,13], then you will get the natural componentwise results from 2*a and a+b and sin(b). A special ``dot notation'' is used for componentwise multiplication and exponentiation: try a.*b and b.^2 and a.^b for example. MATLAB will complain if you try to multiply a*b because the dimensions are not right for matrix multiplication, but you can multiply a times the transpose of b via a*b' (try it).

Remember the struggle you had to implement a Caesar cipher of shift 5 in Maple? Look how easy it is in MATLAB:

>> myword='supercalifragilisticexpialidocious'

myword =

supercalifragilisticexpialidocious

>> secretword=setstr(rem(myword+5-97,26)+97)

secretword =

xzujwhfqnkwflnqnxynhjcunfqnithntzx

>> undecodedword=setstr(rem(secretword-5-97+26,26)+97)

undecodedword =

supercalifragilisticexpialidocious

Explanation: MATLAB automatically converts the letters in a string to their ASCII decimal equivalents if the string is used in a numeric context. Since the letters ``a'' to ``z'' are in ASCII positions 97 through 122, I subtract 97 to get into the range 0 to 25, then I add 5 to apply the shift, then I take the remainder (the function rem) upon division by 26 (this amounts to reducing modulo 26), then I add 97 to get back into the range 97 to 122, then I convert back to a string with the setstr function. This encodes the message. I decode by reversing the operations. Improvements to this cipher are left as an exercise!

Here are a few examples of commands to make three-dimensional graphics in MATLAB.

x=-2:0.1:2; y=x; [X,Y]=meshgrid(x,y); % define planar grid

Z=sin(X.*Y); % define a function

mesh(X,Y,Z) % plot function wireframe style

surf(X,Y,Z) % plot function patch style

waterfall(X,Y,Z)

colormap(gray),surfl(X,Y,Z),shading interp

For more about 3-D plots, try help matlab/plotxyz. For more about MATLAB in general, issue the command demo after starting MATLAB. To exit MATLAB, type quit.

Final thoughts on learning and teaching

To teach is to learn twice. ---Joseph Joubert, Pensées

When I was an undergraduate, I would sometimes wander about in the stacks of Widener library. Occasionally I would pull a book off the shelf, blow the dust off it, open the cover, and discover that the book had not been checked out for over a hundred years. It was almost a religious experience to meditate in the gloam of the stacks on the immensity of knowledge contained within the walls of the library.

Knowledge is sterile, however, until someone opens the book, extracts the ideas, and reinvests them with new life. Those old authors surely had in mind, when they took pen in hand, that they were only the initial link in a chain of communication whose terminus was beyond sight.

One of my goals in this course was to remind you of something that you all knew as four-year-olds: learning and teaching are fun. It is my hope that as your career progresses, you will spread the message by example to your own students and colleagues.

I once took a course in quantum mechanics from Sidney Coleman, whom I remember as a flamboyant lecturer. He made a point, at the end of each class, of dropping his notes into the wastebasket. He did not preserve his lecture notes for use in future years because, he said, ``I don't want to get stale.''

Envoi

And gladly wolde he lerne and gladly teche. ---Chaucer, The Canterbury Tales

Up: Class 13, Math 696
Next: Homework
Previous: Goals

Created Oct 13, 1996. Last modified Dec 4, 1996 by boas@tamu.edu.
URL: /~harold.boas/courses/696-96c/class13/activities.html
Copyright © 1996 by Harold P. Boas. All rights reserved.