One of the advantages of using LaTeX for preparing documents is that LaTeX is highly portable: it is easy to transfer LaTeX files to another computer system, and they will produce just about the same printed output on different machines. However, today we are going to work with graphics, and unfortunately there is no standard format for graphics. Therefore, some of what you do today will not transfer automatically to other computers. You may not be able to get the same results on your home PC, for example.
LaTeX has a built-in picture environment that is
machine-independent, but this environment is suitable only for
simple pictures made of lines, circles, and spline curves. For
more sophisticated graphics, you need to use the add-on
graphics package by putting the command
\usepackage{graphics} in the preamble of your LaTeX
document.
The effects you can achieve with the graphics
package depend on your printer. Today we are going to see what
can be done with a PostScript printer. (The TAMU UNIX machines and
the Mathematics Department machines all output to PostScript
printers.) Therefore we are going to use the
graphics package with the dvips option,
like this: \usepackage[dvips]{graphics}.
Cut out the following lines with the mouse and use a text editor
to change
the information to apply to yourself. Then save the file as
test.tex, open a terminal window, run latex
test and dvips test. Then start the PostScript
screen previewer via ghostview test.ps &. What
do the LaTeX commands \rotatebox and
\reflectbox do?
\documentclass[12pt]{article}
\usepackage[dvips]{graphics}
\begin{document}
This is a test of the graphics package.
What does \rotatebox{30}{my name} do?
What does \reflectbox{a secret message} do?
\end{document}
Rotating text is a special effect that should be used sparingly. More useful is the capability to include graphics that some other program has created. For example, you can include a Maple plot in a LaTeX file. Here is an example.
Open up Maple and execute the command plot3d((1.3)^x * sin(y), x=-1..2*Pi, y=0..Pi, coords=spherical, style=patch);
When the plot window opens, click on File,
then on Print, then on
PostScript. Click on Confirm, and Maple
will save the plot as a PostScript file named
plotoutfile.ps. Close the plot window.
Use
your text editor to open the file test.tex that you
created above, and add the command
\scalebox{.25}{\rotatebox{-90}{\includegraphics{plotoutfile.ps}}}
just before the \end{document} statement.
Save your file, run latex test, dvips test, and ghostview test.ps & to preview the result on the screen. You should see the Maple plot showing up in your LaTeX document.
Now try putting the command \resizebox{0.75\textwidth}{!}{\rotatebox{-90}{\includegraphics{plotoutfile.ps}}} in your LaTeX document, and repeat the previous step.
Can you figure out what these LaTeX commands are doing? By default, Maple saves plots as full-page images in landscape mode. That is the reason in the above example for rotating and scaling the included graphic.
It is possible to coax
Maple into rotating and scaling the image before saving it to a
PostScript file. If you give Maple the command
plotsetup(postscript, plotoutput=`myplot.ps`,
plotoptions=`portrait,noborder,height=200,width=200`);
for example, and then re-execute the plot command, Maple will
directly save the plot (without opening a plot window) to a
PostScript file named myplot.ps in portrait
orientation, with no border, and with height and width of 200
points (where 1 inch is 72 points). Then in your LaTeX file, you
could just put the command \includegraphics{myplot.ps}
without using the \scalebox and \rotatebox
commands.
Note that the plotsetup command affects the whole
Maple session. If you want to save several plots, you need to
issue several plotsetup commands with different
values specified for plotoutput. To make Maple
revert to displaying plots on the screen, issue the command
plotsetup(x11); to restore the default behavior under
x-windows. (Maple V Release 4 will have a new command
plotsetup(default); to restore the defaults under any
operating system.)
This is an exercise to practice incorporating Maple plots into LaTeX documents. Begin the exercise in class and finish it for homework.
The mathematics in the exercise comes from the following article:
Frank A. Farris
Wheels on Wheels on Wheels---Surprising Symmetry
Mathematics Magazine, 69 (1996), number 3, 185-189.
Start by examining the plot generated by the following Maple commands.
x := t -> cos(t) + cos(7*t)/2 + sin(17*t)/3; y := t -> sin(t) + sin(7*t)/2 + cos(17*t)/3; plot([x(t), y(t), t=0..2*Pi], axes=none, thickness=3, color=green);
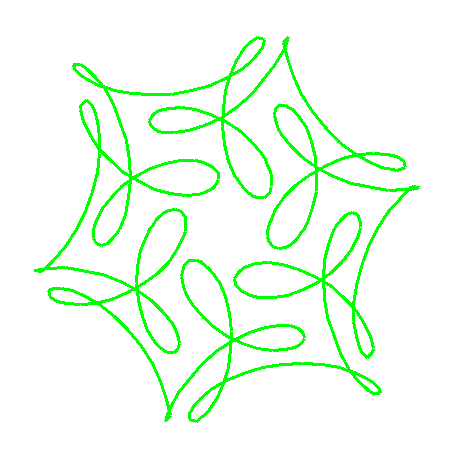Your plot should look something like the figure. Notice that it
has six-fold symmetry. Figure out why you should be able to tell
ahead of time from the equations that this symmetry is
present. (Hint: the numbers 7 and -17 are both congruent to 1
modulo 6.)
The physical interpretation is that the curve represents the
position of a particle on a wheel whose center is mounted on the
rim of a second wheel whose center is mounted on the rim of a
third wheel, each wheel turning at a different rate.
Do you remember Euler's formula about complex exponentials? It says that eit = cos(t) + isin(t). You can get the above plot using complex exponential notation as follows.
z := t -> exp(I*t) + exp(7*I*t)/2 + I*exp(-17*I*t)/3; plot([Re(z(t)), Im(z(t)), t=0..2*Pi], axes=none, thickness=3, color=green);
Next try plotting the curve given in exponential notation by z(t) = e-2it + (1/2)e5it + (1/4)e19it. How can you tell from the equation that the plot has 7-fold symmetry?
Your assignment is to write a LaTeX document explaining the symmetry of such figures and displaying some pretty plots of your own devising. (For example, can you find an attractive plot with 9-fold symmetry?) Be sure to identify the function that generates each figure you include in your paper.
Comments to Harold P.
Boas.
Created Oct 2, 1996.
Last modified: Thu Aug 4 15:27:48 EDT 2022