This problem is related to the problem we worked in class about two intersecting cylinders.
Consider three cylinders of unit radius, one with axis along the x-axis, one with axis along the y-axis, and one with axis along the z-axis. Coerce Maple into producing a reasonable picture, and compute the volume of the intersection of the three cylinders.
Typeset your solution, with picture.
To solve this problem, you will want to use the formula from class for the volume of a ball in n-space.
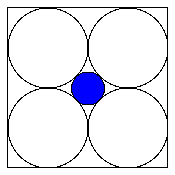
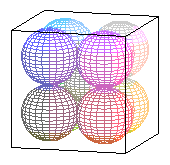Consider a unit
square with circles drawn in its corners, the circles being as
large as possible without overlapping; and look at the largest
circle centered at the origin that does not overlap any of the
other circles. In three dimensions, the analogue
would be a cube with spheres drawn in its eight corners, and a
central sphere as large as possible without overlapping the
spheres in the corners. (See the figures.)
Consider the corresponding situation in n dimensions. Problem: what happens to the volume of the central sphere as a function of the dimension n when n goes to infinity?
This problem gives a beautiful illustration of how it is easy to guess incorrect limits using the computer. Try computing with Maple to find the volume for dimensions up to 100. What do the numbers suggest for the limit? Now try dimensions 1000 and 1200; what does it look like now? Now try dimension 1300 for a surprise.
Typeset a solution to the problem.
Continue to work on Project A (your home page) and on Project B (your Maple lab).