Math 696 -- The lost labor of Hercules

According to Greek mythology, Eurystheus required Hercules to accomplish a sequence of apparently impossible tasks--the labors of Hercules. Although Hercules performed 12 labors, two of these were nullified for alleged violations of rules.

Modern scholarship has uncovered a 13th Herculean labor, previously unknown: the lost labor. This task was the glazing of the amphora of Zeus.

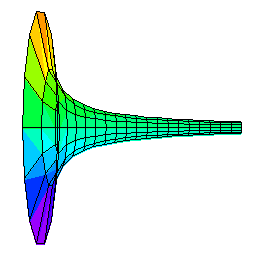The amphora of Zeus had an unusual shape: its cross section at each position x larger than 1 was a circle of radius 1/x (see the figure). The task of Hercules was to paint a liquid glaze on the inner surface of the amphora in preparation for firing it in a kiln.

Hercules realized that a slice of the amphora of width dx at position x would be a ring of radius 1/x and of effective width ds. Hence the surface area of the amphora would be the integral from 1 to infinity of 2 pi/x times dx times the square root of 1 + x^-4. This integral evidently exceeds the integral of 2 pi/x times dx, which diverges. Therefore the task of glazing the amphora is impossible: the amphora has an infinite surface area.

Luckily, Hercules had the happy thought to compute also the volume of the amphora. The slice at position x is a disk of radius 1/x, and hence of area pi/x². Therefore the volume of the amphora is the integral from 1 to infinity of pi/x², which is a convergent integral with the value pi.

Hercules cleverly poured pi units of glaze into the amphora, filling it. Then he poured out the glaze, leaving a residue coating the inner surface. Thus was the impossible task accomplished.

Exercise

That an object can have an infinite surface area but a finite volume seems a paradox. A common explanation of the paradox is that comparing area to volume is like comparing apples to oranges: area is measured in square meters, but volume is measured in cubic meters, so why should there be any correlation between the two? Students generally find this explanation unsatisfying. Can you find a better one?

Write an explanation, suitable for a calculus student, of what is wrong with the solution of Hercules.

Historical note. The amphora of Zeus is more commonly known as Gabriel's Horn. According to Leonard Gillman, the paradox of a container that does not hold enough paint to cover its surface was invented by the mathematics faculty at Columbia University in the spring of 1941; see The College Mathematics Journal 28 (1997), number 5, 379-380. Evangelista Torricelli computed the volume of Gabriel's Horn already in 1641 by using Cavalieri's principle; see Julian F. Fleron, "Gabriel's Wedding Cake", The College Mathematics Journal 30 (1999), number 1, 35-38. Fleron proposed the discrete model shown (truncated) in the figure: a wedding cake that you can eat but not frost.