Math 696 -- Losing your marbles in hyperspace

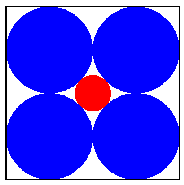Suppose you place four quarters in a square arrangement, as indicated in the diagram. The space left in the middle is quite small: a dime is much too big to fit into it.

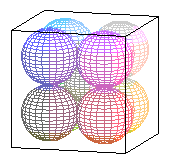Similarly, if you put eight marbles in the corners of a cube, then the largest marble that fits in the space in the middle is again much smaller than the marbles you started with.

In general, suppose you put n-dimensional "marbles" in the corners of an n-dimensional "cube". When n becomes large, what happens to the size of the largest marble that fits in the middle?

To give a sensible answer, we first need to make a normalization. Suppose the enclosing "cube" has sides of length 1, so that the cube has volume 1. Each of the marbles in the corners of the cube then has diameter 1/2 or radius 1/4.

If you ask a typical mathematician unfamiliar with this problem to guess what happens to the volume of the marble in the middle when the dimension n tends to infinity, you will likely get either the answer 0 or the answer 1. The truth is much stranger.

By the n-dimensional Pythagorean theorem, the length of the diagonal from the center of the cube to a corner is 1/2 of the square root of n. Subtracting the diameter 1/2 of the marble in the corner and dividing this difference by 2 gives the radius of the central marble, which is thus (n^1/2-1)/4.

Consequently, when the dimension n=9, the central marble has radius 1/2, and so extends out to the edge of the enclosing cube. When the dimension n exceeds 9, the central marble actually extends outside the "enclosing" cube! Indeed, the radius of the central marble grows without bound when n tends to infinity. The shape of high-dimensional space challenges our intuition.

On the other hand, we saw previously that the volume of a unit ball in n-dimensional space tends to zero when the dimension increases. So it is not immediately clear what happens to the volume of the central marble when the dimension tends to infinity.

Exercise

Define a function g(n), the volume of the central marble in the n-dimensional situation described above. Check your formula against the values g(2)=0.033688 and g(3)=0.025676.

We are interested in what happens to g(n) when n becomes large. Run the Maple loop "for n from 2 to 20 do evalf(g(n)) od;" and guess the limit of g(n) when n goes to infinity.

Now run the Maple loop for n from 100 to 120 do evalf(g(n)) od;. Does this reinforce your guess?

Now run the loop for n from 1000 to 1020. Does this change your opinion?

Now try n from 1500 to 1520. What is your guess now? Can you prove it?

What lesson is there here about making inferences from numerical data?

As mentioned before, volumes of balls in different dimensions are not comparable, for they are measured with different units. It would be more appropriate to compare the values of g(n)^1/n as the dimension n varies. If you know Stirling's formula for the asymptotic behavior of the Gamma function (or of the factorial function), then you can show that g(n)^1/n tends to the limit (e pi/8)^1/2. The ultimate explanation of the mysterious behavior of the swelling marble is that the product of pi and e happens to be (slightly) larger than 8.