| Some exercises on two-dimensional Maple plots |
Caution is appropriate when interpreting graphs drawn by a computer. For example, the exponential function is never equal to zero, but the Maple plot command
plot(exp(x),x=0..7, tickmarks=[0,0],
thickness=3);
produces a graph that certainly looks like it goes through the origin! The following exercise is another illustration of how careless use of the computer can obscure critical details of a problem.
Exercise: Seeing is believing--or is it?
This problem is due to Benny Evans and Jerry Johnson, Uses of Technology in the Mathematics Curriculum, as quoted by George B. Thomas and Ross L. Finney in Calculus, eighth edition, page 235:
Find the local extrema and inflection points of the graph of the function f(x) = (1/8)x8 - (1/2)x6 - x5 + 5x3.
First try plotting the function for -10<x<10.
Although this function is a simple polynomial, the computer is going to mislead you unless you pay attention to the questions you ask it. You may want to adjust the horizontal and vertical ranges of your plot, and you may want to ask Maple to solve for the points where the derivative is equal to zero. If you zoom in on the critical points, one of them may surprise you.
Exercise: Lemniscate
Learn about Maple commands for parametric plots and polar plots by reading the online help obtained by issuing the commands ?plot[parametric] and ?plots[polarplot] at the command prompt in a Maple window (or read the same information in a printed Maple manual).
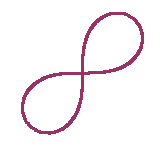 Now try to reproduce the plot shown in
the figure
of the lemniscate
with polar equation r2=sin(2 theta). Due to the squared
term, it is tricky to create this plot. Your first try will
probably give a curve that does not connect at the origin.
Now try to reproduce the plot shown in
the figure
of the lemniscate
with polar equation r2=sin(2 theta). Due to the squared
term, it is tricky to create this plot. Your first try will
probably give a curve that does not connect at the origin.
Incidentally, the plot shown was created with the following plot
options:
thickness=3, scaling=constrained,
color=maroon (among others).
Here is another way to dress up the plot: superimpose it on a colored background. Define your lemniscate plot as plot1 and then use the command plot2:= polygonplot([[-2,-2], [2,-2], [2,2], [-2,2]], color=cyan, axes=none): to define a colored square. Now try display([plot1,plot2]); to view your plot on a cyan background.
Exercise: The imaginary can
Exercise 12 of Chapter 3 of the CalcLabs with Maple manual reads as follows:
A cylindrical can with a top and bottom is to contain 1000
cubic centimeters. Find the dimensions of the can if its
surface area is 600 square centimeters.
Note: there are two
answers.
Consider the following alleged Maple solution to the problem.
Let r and h denote the radius and the height of the cylinder. We set up a pair of simultaneous equations and solve them for r and h.
> eq1:=Pi*r^2*h=1000:
eq2:=2*Pi*r^2+2*Pi*r*h=600:
fsolve({eq1,eq2},{r,h});
{r = -11.13867027, h = 2.565567417}
Obviously something is wrong here, because it does not make sense for the radius to be negative!
Write a Maple worksheet, addressed to an audience of first-year calculus students, that explains the error and exhibits a correct solution. Use Maple's Print feature to get hard copy.
Include an appropriate Maple plot to illustrate what is going on and where the spurious answer came from. (If your plot is displaying in a separate window instead of inside the worksheet, look on the Options menu for Plot Display, and select Inline.)
 The Math 696 course
pages were last modified April 5, 2005.
The Math 696 course
pages were last modified April 5, 2005.| Some exercises on two-dimensional Maple plots |