
Last time many people reported problems printing from
Mosaic. The system administrator for the CalcLab has modified the
configuration, so printing from Mosaic should now work. From the
File drop-down menu, select Print and
choose PostScript format; there are check-boxes to
toggle whether or not the printout has an identifying headline
(banner) and whether or not footnotes print to give the Web
addresses of links.
Some people prefer to use Netscape as a Web browser. You can start Netscape by executing the command netscape & in a terminal window.
When you worked on the homework, did you notice that the
Maple command
evalf(int(1/(1+x^2),x=0..infinity),30); actually
gives the answer to 29 decimal places, not 30? Why is this?
Consider the output of the Maple commands evalf(Pi,4);
evalf(Pi,5); evalf(Pi,6);. If someone asks you for the
value of Pi accurate to four decimal places, what is the best
answer? Why?
When you have an answer that everybody in your group is happy with, you can all jump up in unison and shout ``Pie are square.''
Trade your homework papers on the topic ``Why study math?'' between groups.
Based on your reading of the papers by Group 3, formulate two good things to do in writing a paper, and two things to avoid.
Decide which of the papers by members of Group 2 is the best one, and why.
When you have finished, you can all stand up and start doing the Macarena.
You probably have accounts on more than one computer. If you
are a graduate student in the Mathematics
Department, you have accounts on both the
calclab machines and on the main mathematics
server. If you are a student in another department, you may have
an account on tam2000 as well as on the calclab
machines.
You might like to arrange for all your mail to be forwarded automatically to the account you check most often. Or you might like to keep a copy of each incoming mail message in the account to which it is addressed, and also forward a copy to the account you use most often. My howto on mail forwarding explains the procedure to accomplish this.
Sometime today---don't everybody do it at once---you should change your initial, randomly generated password.
You should choose a new password that is easy for you to remember, but that is hard for another person (or a computer program) to guess. Therefore, your password should not be a word and should not be closely related to a word. For example, ``calculu2'' and ``suluclac'' are bad passwords.
A good password should normally be eight characters long and should contain a mix of lowercase and uppercase letters and numbers. (Passwords longer than eight characters are accepted, but typically only the first eight characters are active.) Some examples of good passwords:
This comes from taking the initial letters of the sentence ``We have nothing to fear but fear itself,'' changing one letter to a digit, and capitalizing a random letter.
This is the initials of the members of my brother's family followed by the last two digits of their zip code.
This is two syllables extracted from the words ``Diophantine approximation'' and spliced together with a digit.
Of course, these particular examples are no longer good passwords since they have been published.
On the calclab machines, there is a utility
program to help you change your password. Click the mouse on the
background to bring up the root menu, click on
Utilities, and click on Change
Password. Then follow the prompts. You will be asked to
enter your current password first, and then to enter your new
password twice (to guard against typing errors).
Note to experienced users: there is a UNIX
passwd command that can be used at the command
prompt in a terminal window to change passwords. You probably do
not want to use this command, because you could end up with
different passwords on the different calclab
machines (calclab1, calclab2,
calclab3, calclab4).
Most word processors on personal computers are ``what you see is what you get'' (WYSIWYG) programs. For example, if you want a word to print in italic (slanted) type, you click a button or make a menu selection, and the characters change their appearance right on the screen. With a markup language like LaTeX, you instead insert special control sequences into your document that code the instructions to change the type style, but you do not see the result until you run a separate preview program or print the document.
Why is it useful to use the second method instead of the first? There are several reasons.
With a markup language, you are forced into using a consistent
style. For example, if you start each section of a document with LaTeX's
\section command, you can be sure that all section
headings will have the same font. With a WYSIWYG program, you
might instead end up with section headings in several different
font styles; this would be a particular problem if you were to
merge two WYSIWYG documents written by different authors.
With a markup language, it is easy to change the style throughout
a document. Suppose you need to change all the italic words to
underlined words. With a WYSIWYG program, you would have to go
through the whole document by hand to locate and change each
occurrence of italic text. With a program like LaTeX, you could
use the global search-and-replace feature of your editor to
change all occurrences of \emph to
\underline with a single command. Even better, you
could simply insert one line of code at the beginning of your
LaTeX document to redefine \emph to be a synonym for
\underline.
Thus, a markup language is more flexible than a WYSIWYG program if you want to make changes to the style. For this reason, devotees of markup sometimes disdainfully refer to WYSIWYG as ``what you see is all you've got.''
Perhaps the most important feature of markup languages is that they encourage you to concentrate on the logical structure of your document rather than on its visual appearance. In the past, most documents were printed on paper. In the modern technological world, your documents may instead be read on a computer screen, and you cannot know ahead of time what size the screen is or what fonts are available to the viewer; or maybe your document will be ``read'' by a blind person using a speech synthesizer. Therefore, you do not want your document to have instructions like ``set these characters in 14 point bold Helvetica type''; instead, you should say something like ``this is a level 2 section header.''
The most common language used for documents on the World-Wide Web is a markup language called HTML, which stands for ``Hyper-Text Markup Language.'' A simple example will show that HTML is quite similar in philosophy to LaTeX.
Consider the following short LaTeX document.
\documentclass{article}
\setlength{\textwidth}{5cm}
% the above command makes a narrow
% page width for demonstration purposes
\begin{document}
\section{Getting started}
Learning the news of Napoleon's
defeat at Borodino,
Talleyrand is
supposed to have said:
\begin{quote}
\emph{Voil\`a le commencement de la fin.}
\end{quote}
In English, this means: ``This is the beginning of the end.''
\end{document}
If you cut this example out with the mouse, paste it into your
text editor, save the result as example.tex, run the
command latex example, and then preview the result via
the command xdvi example, you should see something
like the following.

Run the above example through LaTeX and preview it or print it. The output actually is not quite identical to what is shown above. The bottom line is that I told you 1 small fib. When you are convinced that you know what it is, you can all jump up in unison and shout ``Eureka!''
Now let's see how this example would be coded in HTML:
<HTML> <HEAD><TITLE>An example</TITLE></HEAD> <!-- the title normally displays in the browser's title bar --> <BODY> <H1>Getting started</H1> <P> Learning the news of Napoleon's defeat at Borodino, Talleyrand is supposed to have said: </P> <BLOCKQUOTE> <P><EM>Voilà le commencement de la fin.</EM> </P></BLOCKQUOTE> <P> In English, this means: ``This is the beginning of the end.'' </P> </BODY> </HTML>
Here is how the Web browser will format this HTML code:
Learning the news of Napoleon's defeat at Borodino, Talleyrand is supposed to have said:
Voilà le commencement de la fin.
In English, this means: ``This is the beginning of the end.''
Compare the HTML code with the formatted output to get an idea of how HTML works. Notice that HTML markup ``tags'' come in pairs marking the beginning and the ending of a logical structure: for example, <EM>this is emphasized text</EM>. Tags are surrounded with angle brackets, and the end tag differs from the start tag by having a forward slash / (not to be confused with the backslash \ that LaTeX uses to mark its control sequences).
HTML has six levels of section headers, labeled H1 through
H6. Unlike LaTeX, which uses a blank line to signal a new
paragraph, HTML insists on paragraphs being marked explicitly
with the <P> tag. In general, HTML ignores extra white
space in the input file. To mark special character entities, HTML
uses special sequences of characters starting with an ampersand
and ending with a semicolon: for example,
é turns into é and
ö turns into ö (LaTeX would code these
as \'e and \"o).
Your first project for the semester is to build a World-Wide Web home page. Today we are going to get started on this project. During the semester, you will add links and images and further information to the page, but today the goal is just to get a page that works.
Here is a template for a very basic Web page. Use the mouse to cut out this template and to paste it into a text editor. Then modify the information to apply to yourself. Since blank lines do not start new paragraphs, you can use blank lines to make your input file more readable. (You must use an explicit <P> tag to start a new paragraph.)
<html>
<head>
<title>A sample home page</title>
</head>
<body>
<h1>A. Student's Home Page</h1>
<P> Here is some information about me.
The paragraph end tag is optional.
<P>But remember that a P tag is needed to start a new paragraph.</P>
<h2>This is a level two header</h2>
<OL>
<LI>This is the first item of an ordered list.
<LI>The list item tag LI is another one that has an optional
end tag.</LI>
</OL>
<h3>Information about me</h3>
<ul>
<li>My e-mail address
<li>My telephone number
<li>And so on; this is an unordered list.
</ul>
</body>
</html>
The Web browser will format the above code like this:
Here is some information about me. The paragraph end tag is optional.
But remember that a P tag is needed to start a new paragraph.
After you edit the HTML template, you need to save it as a
file and make sure that Web browsers can find it. Each computer
system has a special location where it expects to find publicly
accessible HTML files. On the calclab machines and
the main mathematics server, the location for HTML files is a
subdirectory named public_html in your home
directory; this subdirectory has probably already been created
for you with the correct access permissions by the system
administrator. (On tam2000, the subdirectory is
named .public_html with an initial period; you will
have to create it yourself and make it world-readable and
world-executable.)
Save your basic home page in this special subdirectory with
the name index.html (this is a standard name for home
pages). Use the Save As feature on your text editor: you can
probably navigate to the subdirectory public_html
with a mouse click, and then type in the name index.html.
There is one more step: you need to change the access permissions
on index.html to make it a world-readable file. Open
a terminal window, execute the command cd public_html
(on tam2000, cd .public_html)
and then the command chmod a+r index.html.
Now test it out. In a Web browser (Mosaic or Netscape),
click on the Open button, and type in
http://calclab.math.tamu.edu/~your_user_id/ (if your
home page is on the calclab machines) or
/~your_user_id/ (if your home
page is on the main mathematics server) or
http://http.tamu.edu:8000/~your_user_id/ (if your home
page is on tam2000). Your home page should display
in the browser. Now have your neighbor try to display your home
page (this is an extra check to confirm that the file permissions
are set correctly).
When you have time to go further, you can look at some information for building home pages from the local Web Beginner's Corner, and you can investigate some of the html resources on our class list of resource materials. Other tips:
There is a free automated validator that will find syntax errors in your html code.
If you see a Web page you like, and you are wondering
``How did they do that?'', you can examine the html source code
by clicking on View and Source (in
Netscape) or File and View Source (in
Mosaic).
Work through chapter 2 of the CalcLabs with Maple V manual.
In other words,
find p(n) of the form
a*n3+b*n2+c*n+d
such that p(1)=2, p(2)=3, p(3)=5, p(4)=9. You can
do this by setting up four simultaneous linear equations
in the four unknowns a, b, c, d and using Maple's
solve function; then you can use Maple to
substitute the values of a, b, c, d back into
p.
Look in Maple's help browser for commands related to interpolation. See if you can find a single simple Maple command that will solve the above problem in one step.
Go back and edit your Maple worksheet to clean up the
presentation. Put in some sentences of explanation. (From
the Edit menu, you can click on Insert
Text to put in
textual comments before or after Maple commands.) In
particular, put your name at the top of your worksheet.
Print your worksheet and turn it in during class. (From
the File menu, click on Print,
click on the Printer
Command button, and click OK.)
In the next class, you will write a paper in LaTeX with mathematical equations. Here is some information about how to format equations with LaTeX. You may read this information after class if you do not have enough time during class.
When you wrote your paper on ``Why study math?'', you may not have seen any advantage in using LaTeX rather than the word processor you are used to. (If you have some typesetting experience, however, you may have noticed how nicely LaTeX justifies lines and how clever it is about hyphenating words.) It is in the formatting of mathematical equations that LaTeX really shines. Indeed, the program TeX that underlies LaTeX was created by Donald E. Knuth (a mathematician and computer scientist) with the needs of mathematicians in mind.
Equations come in two flavors: short in-line equations that do not interrupt the paragraph, and displayed equations that are printed on a separate line. All mathematical formulas are enclosed between special delimiters that signal LaTeX to switch to its special mathematics mode.
For example, here are three equivalent ways to write the same anti-derivative formula from calculus as an in-line equation.
This is an in-line $\int
\frac{d\theta}{1+\theta^2} = \tan^{-1}\theta+C$ equation.
Here mathematics mode is delimited by dollar signs.
This is an in-line \(\int\frac{d\theta} {1+\theta^2}=
\tan^{-1} \theta+C\) equation.
Here mathematics mode is delimited by the \(
and \) pair.
This is an in-line \begin{math}\int\frac {d\theta}{1+\theta^2}
= \tan^{-1} \theta+ C\end{math} equation.
Here the mathematics environment is delimited by the
\begin{math} and \end{math}
pair.
The output as formatted by LaTeX looks like this:
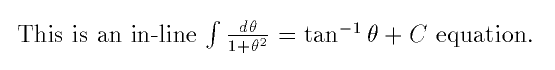
Here are a few points to note about this example.
LaTeX ignores input spaces in mathematics mode. (It spaces formulas according to its own internal rules.)
Standard mathematical functions have natural LaTeX control
sequences: \sin, \cos, and so on
give the trigonometric functions; \int makes
an integral sign; \frac builds a fraction
whose numerator and denominator are the subsequent two
items enclosed in curly braces.
The LaTeX control sequences for Greek letters are their
names preceded by a backslash, e.g., \gamma
produces a gamma, and \Gamma produces a
capital gamma.
LaTeX uses curly braces for grouping and for delimiting
arguments; the braces do not print. (If you really want to
make LaTeX print an opening brace, you would type \{
in your input file.)
A caret ^ makes a superscript, and an underscore
_ makes a subscript.
To format the same formula as a displayed equation that stands on its own line, just change the delimiters. Each of the following produces a displayed equation.
Here is a displayed \[\int\frac{d\theta}
{1+\theta^2}= \tan^{-1}\theta+C\] equation.
Here the \[ and \] pair delimit
display math mode.
Here is a displayed \begin{displaymath}\int\frac {d\theta}{1+\theta^2} =\tan^{-1}
\theta+ C\end{displaymath} equation.
Here the display math environment is spelled out in words.
Here is a displayed \begin{equation}\int
\frac{d\theta}{1+\theta^2}=\tan^{-1}\theta+C\end{equation}
equation.
There is a difference between the displaymath
environment and the equation environment: the latter
automatically typesets a formula number.
The formatted output looks like this:
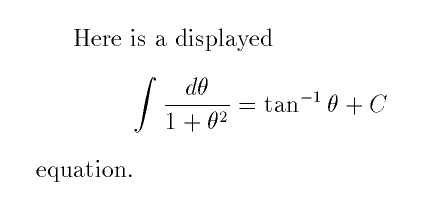
with no formula number, and with a formula number it looks like this:
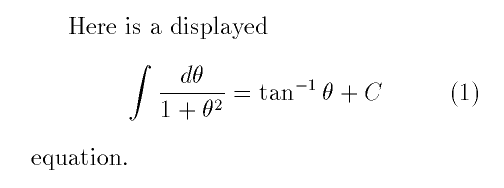
Warning to former plain TeX users: in plain TeX, double
dollar signs $$ are used to delimit display math,
but this convention does not work properly in LaTeX.
Do not use it!
It is a convenient feature of LaTeX that it can automatically generate formula numbers. If you add or delete a numbered equation, you do not have to worry about revising the formula numbers: LaTeX does this chore for you.
What if you want to refer to a numbered equation by number? How
do you manage this if the equation number is automatically
generated? LaTeX has a simple \label and
\ref mechanism for handling symbolic cross
references. Here is an example.
The formula \begin{equation} E=m c^2
\label{Einstein} \end{equation} has passed into popular culture,
but the true significance of the mass-energy
equation~(\ref{Einstein}) is~\ldots
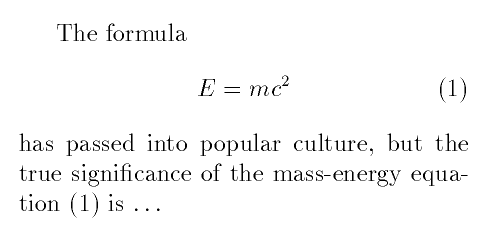
(By the way, that tilde ~ is a
tie or non-breaking space: it is good type-setting style to keep a
short label attached to its noun.)
If you use the amsmath package described below, then you can type
\eqref instead of \ref, and the
parentheses around the cited equation number will be supplied
automatically.
If you are going beyond the most basic level of displayed equations, I recommend that you use the amsmath package that plugs into LaTeX. This has lots of useful features for multi-line equations, compound symbols, even commutative diagrams!
To load this
package, put the command \usepackage{amsmath} in the
preamble of your LaTeX input file. Now you can make aligned
equations, for example, like this:
\documentclass[12pt]{article}
\usepackage{amsmath}
\begin{document}
\begin{align}
\cos^2\psi+\sin^2\psi & = 1, \\
\cosh^2\omega-\sinh^2\omega &=1.
\end{align}
\end{document}
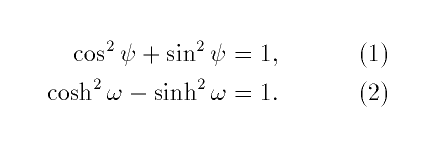
Here the separate
lines of the display are separated in the input file
by a double backslash \\, and
the alignment point(s) are indicated by ampersands
&. Notice the automatically generated equation
numbers; you can suppress the equation numbers via
\begin{align*} ... \end{align*} (the ``star form'' of
the align environment).
The amsmath package was created by the American Mathematical Society and some of the gurus of the LaTeX3 project to augment LaTeX's mathematics capabilities. It is related to, but not the same as, the AMS-TeX macro package that supplements plain TeX. For further information about the amsmath package, you can view the AMS-LaTeX user's guide as a dvi file (looks better on the screen) or as a PostScript file (can be sent to the printer for hard copy). This user's guide is incorporated into Chapter 8 of the LaTeX Companion.
Comments to Harold P.
Boas.
Created Sep 10, 1996.
Last modified: Mon Nov 18 20:56:12 CST 2024