Introduction to LaTeX macros

In computerese, a macro is just a shorthand command that abbreviates a more complicated sequence of commands. For example, LaTeX's \section macro encodes instructions to leave some vertical space, to increment the section number counter, and to set a section header.

Like any self-respecting programming language, LaTeX lets you define your own macros. LaTeX has a \newcommand command that you can use to define personal macros. Why would you want to do this?

Suppose you are writing a document in which you are going to refer to Texas A&M University twenty-five times. To save typing, you might type ``Texas A&M University'' once and then copy it twenty-four times with the mouse.

Unfortunately, you find out when you run the document through LaTeX that LaTeX wanted you to type ``A\&M'' instead of ``A&M.'' Or perhaps you decide later that you want to say ``Texas A&M University System'' instead of ``Texas A&M University.''

By defining a LaTeX macro, you can simultaneously save typing and protect yourself in the event of future revisions. If you type

\newcommand{\tamu}{Texas A\&M University}

then you can later type

Bonfire is a tradition at \tamu.

LaTeX will translate this as

Or you can type

\tamu{} is a land-grant institution.

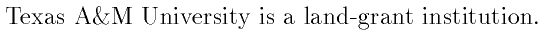
Question: what is the point of the empty braces in the above example? Run a test without the braces to find out.

By using the \tamu macro, you save typing, and you also make it easy to revise your document. If you decide to change ``Texas A&M University'' to ``Texas A&M University System,'' you need only make this change once, in the definition of the macro \tamu.

(Aside to former plain TeX users: LaTeX's \newcommand command is preferable to TeX's \def command, because \newcommand prevents you from accidently redefining an existing macro. If you really do want to redefine an existing LaTeX command, and you are sure no disaster will ensue, you can do this via LaTeX's \renewcommand command.)

Here is another example. See if you can determine what the following LaTeX file will produce. Then cut the example out with the mouse, paste it into a text editor, save it as goose.tex, and run latex goose and xdvi goose & to see if you are right.

\documentclass[12pt]{article}

\title{A rhyme from Mother Goose}

\newcommand{\pea}{Pease porridge}
\newcommand{\heiss}{hot}
\newcommand{\kalt}{cold}
\newcommand{\pot}{in the pot nine days old}
\newcommand{\some}{Some like it}

\begin{document}

\maketitle

\begin{verse} 
\pea{} \heiss,\\ 
\pea{} \kalt,\\ 
\pea{} \pot.\\ 
\some{} \heiss,\\ 
\some{} \kalt,\\ 
\some{} \pot.  
\end{verse}

\end{document}

Here is a (slightly) less silly exercise for you to try. Suppose that you have just received (lucky you!) a number of gifts on some special occasion: a birthday, or a baby shower, or a wedding. Now you have the social obligation of writing ``bread and butter'' notes of thanks.

Take the following letter template and use \newcommand to define all the control sequences containing capital letters. (Do not define any of the control sequences having no capital letters, for they are all internal LaTeX commands.) Then save your letter as butter.tex and run latex butter and xdvi butter & to see what your thank-you note looks like. (This is our first example of using a \documentclass other than article.)

\documentclass[12pt]{letter}

%% Put your \newcommand statements here.
%% For example:
\newcommand{\MyName}{Don Joe}

              
%% Do not make any changes below this line!

\address{\MyStreetAddress\\ 
         \MyCity}
\signature{\MyName}

\begin{document}

\begin{letter}{}

\opening{Dear \GiftGiver,}

\ExpressionOfGratitude{} for the \Adjective{} \Gift.
It is just what I need to give a special touch to my \LivingQuarters.

Whenever I look at your \Gift, I will think of you \Adverb.

\AnotherExpressionOfGratitude.

\closing{\ClosingAdverb,}

\end{letter}

\end{document}

Here is a sample of what the output might look like.

A more practical use for macros is to simplify the typing of mathematical formulas. Suppose that you need to type many times. You might make a definition like \newcommand{\gijk}{\Gamma^{ij}_k} and then type \gijk each time you want to use this symbol (inside mathematics mode).

It is a common error to forget to open or close mathematics mode, so LaTeX provides a crutch in the form of the \ensuremath command. If you modify the above macro definition to \newcommand{\gijk}{\ensuremath{\Gamma^{ij}_k}}, then LaTeX will interpret \gijk outside of mathematics mode as if it were $\gijk$ (and LaTeX will still do the right thing when you use \gijk inside mathematics mode). This should save you from a few error messages in the future!

Next suppose that you want to typeset the symbol with different indices, say r, s, and t. You could make a new definition \newcommand{\grst}{\Gamma^{rs}_t}, but if you are going to be using many different subscripts and superscripts, then it gets tedious to define a new control sequence for each set of indices. What you need is a macro with replaceable parameters.

If you type \newcommand{\christoffel}[3]{\ensuremath{\Gamma^{#1#2}_{#3}}}, then LaTeX treats \christoffel as a command that expects three arguments (the [3] tells the number of arguments). LaTeX knows to fill in the first argument where it sees #1, the second argument where it sees #2, and so on (you can have up to nine arguments). In this example, the first two arguments are set as superscripts to the capital Gamma, and the third argument is set as a subscript. Thus, \christoffel{i}{j}{k} gives and \christoffel{gig}{em}{aggies} gives . What happens if you type \christoffel{gig}{em}aggies by mistake?

A fancier possibility is a macro whose first argument is optional. Suppose you are going to use lots of Christoffel symbols, but the first superscript is usually going to be i. Then you could type \newcommand{\christoffel}[3][i]{\ensuremath{\Gamma^{#1#2}_{#3}}}. This tells LaTeX that the first of the three arguments defaults to i if it is not specified. So now \christoffel{j}{k} yields , while \christoffel[gig]{em}{aggies} yields .

An exercise on macros to turn in today

Here is an exercise to practice using macros. Your task is to typeset the following monstrosity, described by Michael Spivak in his book The Joy of TeX as ``a virtual mine field of potential typing errors.'' Use \newcommand to define macros to simplify the typing.

Here are two stylistic points to keep in mind.

1. In compound fractions, the second-level fraction tends to be too small. If you type the second-level fraction as \displaystyle\frac instead of \frac, it will be bigger. (If you \usepackage{amsmath}, then you can type \dfrac instead of \displaystyle\frac.)

2. To get parentheses that adjust themselves to the size of the enclosed material, use \left( and \right) instead of just ( and ).

Comments to Harold P. Boas.
Created Sep 24, 1996. Last modified Sep 25, 1996.