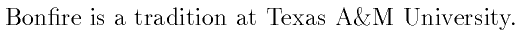
Today's class has a different structure from previous classes. We will spend part of the time in the lecture room and part of the time in the computer lab.
So far we have concentrated on computer technology. We have been learning by the "total immersion" method (also known as the "sink or swim" method). You may have been shocked on the first day of class when I put you in front of a terminal and told you to write a paper in LaTeX. I hope that now, after perhaps floundering around a bit, you feel able to stay afloat on the computer and even enjoy swimming around in cyberspace.
At this point, you all have a basic knowledge of how to get mathematics onto paper via LaTeX; of how to use Maple for numerical, algebraic, and graphical manipulations; and of how to interact with the World-Wide Web. We will be expanding our knowledge of these topics as the course continues. Today, for example, we will learn about one way to customize LaTeX by writing macros.
(A side remark: Some of you are devoted to the axiomatic method in mathematics, and you may feel a desire to learn about the formal rules underlying the computer tools. There exists a precise specification for HTML, for example, and both LaTeX and Maple are programming languages having well-defined data types and syntax rules. You can pursue this direction by consulting some of the materials in the list of class resources.)
One of the most important benefits you can gain from this course is the confidence that you are able to learn new technologies. It is certain that the tools you are learning this semester will change in the next few years, so you need to be comfortable with the idea of adapting as technology progresses. Maple, for example, has a new release coming soon (as some of you learned at the Maple conference here ten days ago). LaTeX is currently being over-hauled by the LaTeX3 project. The World-Wide Web is changing at such a dramatic rate that no one knows where it is going. (It might be that in two years we will all be writing Web pages in Sun's Java language, or in some language that has not been invented yet.)
So far, I have been concentrating on the computer because all of you recognize that this technology is important and useful (and fun!?). Now that we have some basic fluency with the computer, I want to add a new element to the course.
Mathematics is to a large extent a social activity. There are hundreds of mathematics meetings every year. Even Andrew Wiles, today's symbol of the cloistered genius alone in the ivory tower thinking deep thoughts, had to come out of seclusion to discuss his proof of Fermat's last theorem in public.
A significant part of mathematical communication takes place face-to-face, whether in a classroom, or at a research seminar, or on the beaches of Rio de Janeiro. Therefore, we will spend some time discussing and practicing the oral communication of mathematics. Today we will do a warm-up exercise on oral communication.
Today half of you will go to the computer lab while the others stay in the lecture room. Midway through the class period, we will exchange places. Thus, everybody will spend some time at the computer and some time in the lecture room.
In the lecture room, we will do a warm-up exercise on oral communication. Your task is to take a few minutes to prepare an oral presentation on the subject: "Who am I and why am I interested in mathematics?" Then you are going to stand up and give the presentation.
Envision, for example, that during a visit to your home town you have dropped by the high school, and the principal asks you to say a few words to the sophomores. Your presentation should be approximately three minutes long (teenagers have a short attention span), and during the presentation you should at least once write something on either the chalkboard or the overhead projector.
In computer-speak, a macro is just a shorthand command
that abbreviates a more complicated sequence of commands. For
example, LaTeX's \section macro encodes instructions
to leave some vertical space,
to increment the section number counter, and to set a section
header.
Like any self-respecting programming language, LaTeX lets you
define your own macros. LaTeX has a \newcommand
command that you can use to define personal macros. Why would you
want to do this?
Suppose you are writing a document in which you are going to refer to Texas A&M University twenty-five times. To save typing, you might type "Texas A&M University" once and then copy it twenty-four times with the mouse.
Unfortunately, you find out when you run the document through LaTeX that LaTeX wanted you to type "A\&M" instead of "A&M". Or perhaps you decide later that you want to say "Texas A&M University System" instead of "Texas A&M University".
By defining a LaTeX macro, you can simultaneously save typing and
protect yourself in the event of future revisions.
If you type
\newcommand{\tamu}{Texas A\&M University}
then you can later type
Bonfire is a tradition at \tamu.
and LaTeX will translate this as
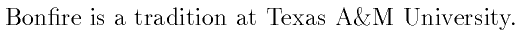
Or you can type
\tamu{} is a land-grant institution.
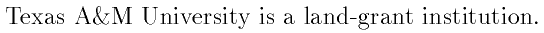
Question: what is the point of the empty braces in the above example? Run a test without the braces to find out.
By using the \tamu macro, you save typing, and you
also make it easy to revise your document. If you decide to
change "Texas A&M University" to "Texas A&M University
System," you need only make this change once, in the definition
of the macro \tamu.
(Aside to former plain TeX users: LaTeX's
\newcommand command is better than TeX's
\def command, because \newcommand
prevents you from accidently redefining an existing macro. If you
really do want to redefine an existing LaTeX command, and you are
sure no disaster will ensue, you can do this via LaTeX's
\renewcommand command.)
Here is another example. See if you can determine what the
following LaTeX file will produce. Then cut the example out with
the mouse, paste it into a text editor, save it as
goose.tex, and run latex goose and
xdvi goose & to see if you are right.
\documentclass[12pt]{article}
\title{A rhyme from Mother Goose}
\newcommand{\pea}{Pease porridge}
\newcommand{\heiss}{hot}
\newcommand{\kalt}{cold}
\newcommand{\pot}{in the pot nine days old}
\newcommand{\some}{Some like it}
\begin{document}
\maketitle
\begin{verse}
\pea{} \heiss,\\
\pea{} \kalt,\\
\pea{} \pot.\\
\some{} \heiss,\\
\some{} \kalt,\\
\some{} \pot.
\end{verse}
\end{document}
Here is a slightly less silly exercise for you to try. Suppose that you have just received (lucky you!) a number of gifts on some special occasion: a birthday, or a baby shower, or a wedding. Now you have the social obligation of writing "bread and butter" notes of thanks.
Take the following letter template and
use \newcommand to define all the control sequences
containing capital letters. (Do not define any of the control
sequences having no capital letters, for they are all internal
LaTeX commands.) Then save your letter as
butter.tex and run latex butter and
xdvi butter & to see what your thank-you note looks
like. (This is our first example of using a
\documentclass other than article.)
\documentclass[12pt]{letter}
%% Put your \newcommand statements here.
%% For example:
\newcommand{\MyName}{Don Joe}
%% Do not make any changes below this line!
\address{\MyStreetAddress\\
\MyCity}
\signature{\MyName}
\begin{document}
\begin{letter}{}
\opening{Dear \GiftGiver,}
\ExpressionOfGratitude{} for the \Adjective{} \Gift.
It is just what I need to give a special touch to my \LivingQuarters.
Whenever I look at your \Gift, I will think of you \Adverb.
\AnotherExpressionOfGratitude.
\closing{\ClosingAdverb,}
\end{letter}
\end{document}
Here is a sample of what the output might look like.
A more practical use for macros is to simplify the typing of
mathematical formulas. Suppose that you need to type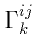 
many times. You might make a definition like
\newcommand{\gijk}{\Gamma^{ij}_k} and then type
\gijk each time you want to use this symbol (inside
mathematics mode).
It is a common error to forget to open or close mathematics mode,
so LaTeX provides a crutch in the form of the
\ensuremath command. If you modify the above macro
definition to
\newcommand{\gijk}{\ensuremath{\Gamma^{ij}_k}}, then
LaTeX will interpret \gijk outside of mathematics
mode as if it were $\gijk$ (and LaTeX will still do
the right thing when you use \gijk inside
mathematics mode). This should save you
from a few error messages in the future!
Suppose that now you want to typeset that symbol with
different indices, say r, s, and
t. You could make a new definition
\newcommand{\grst}{\Gamma^{rs}_t}, but if you are
going to be using many different subscripts and superscripts,
then it gets tedious to define a new control sequence for each
set of indices. What you need is a macro with replaceable
parameters.
If you type
\newcommand{\christoffel}[3]{\ensuremath{\Gamma^{#1#2}_{#3}}},
then LaTeX treats \christoffel as a command that
expects three arguments (the [3] tells the number of arguments).
LaTeX knows to fill in the first argument where it sees #1, the
second argument where it sees #2, and so on (you can have up to
nine arguments). In this example, the first two arguments are
set as superscripts to the capital Gamma, and the third argument
is set as a subscript. Thus, \christoffel{i}{j}{k}
gives 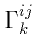and
\christoffel{gig}{em}{aggies} gives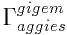 
. What happens if you type
\christoffel{gig}{em}aggies by mistake?
A fancier possibility is a macro whose first argument is optional.
Suppose you are going to use lots of Christoffel symbols, but the
first superscript is usually going to be i. Then you
could type
\newcommand{\christoffel}[3][i]{\ensuremath{\Gamma^{#1#2}_{#3}}}.
This tells LaTeX that the first of the three arguments defaults
to i if it is not specified. So now
\christoffel{j}{k} yields ,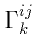
while \christoffel[gig]{em}{aggies} yields .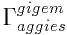
Here is an exercise to practice using macros. Your task is to
typeset the following monstrosity, described by Michael Spivak in
his book The Joy of TeX as "a virtual mine field of
potential typing errors." Use \newcommand to define
macros to simplify the typing.
Here are two stylistic points to keep in mind.
\displaystyle\frac instead of \frac, it
will be bigger. (If you \usepackage{amsmath}, then
you can type \dfrac instead of
\displaystyle\frac.)
\left( and
\right) instead of just ( and ).
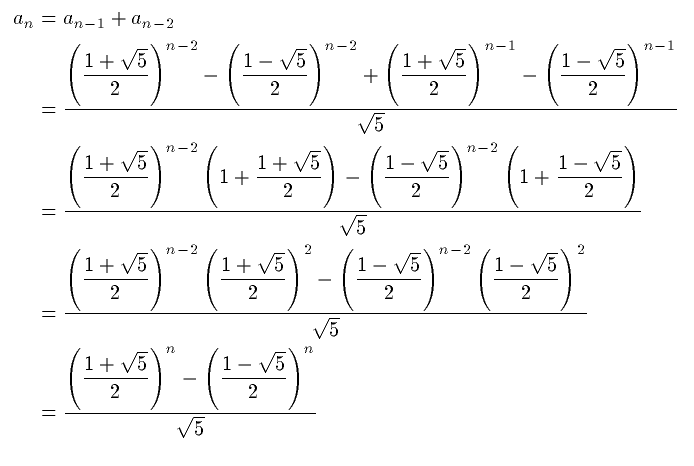
If you want to amaze your friends, try optimizing your LaTeX
code to use as few input characters as possible. (In the real
world, however, it is actually better to write verbose code, so that it is
easier to understand and to revise.) My (not very practical)
LaTeX file for this exercise contains 423 characters, including
everything from \documentclass{article} to
\end{document}. Can you do better? (To determine the
number of characters in a file, open a terminal window and
execute the UNIX command wc filename.
Here wc stands for "word count"; it returns the
number of lines, words, and characters in the specified file.)
There are some nifty programs out there in cyberspace that interact
with you via e-mail. For example, did you know that the letters
in "Texas A&M University" can be rearranged to form
"Anxieties must vary"? The letters in my name, Harold
Philip Boas, can be rearranged to form "Abolish hippo lard!" You
can find your own anagrams by sending e-mail to
wsmith@wordsmith.org with a subject line of
the form anagram string of characters
(the message body is ignored). For example, try anagram your
name.
There is also a list
of WWW based anagram servers at Yahoo.
If you find a funny anagram, post it to the
tamu.classes.math689 newsgroup.
Would you like to build your English vocabulary? Send a
message to wsmith@wordsmith.org with a subject line
subscribe and you will be subscribed to the A Word A
Day mailing list: each morning you will be sent a new word with
its definition.
In addition to automated mail servers, there exist e-mail
discussion lists. These are analogous to newsgroups, except that
messages come to you directly via e-mail. For example, suppose
you want to keep up with the latest developments regarding
Adobe's Acrobat software. You could send a message to
acrobat-request@blueworld.com with a message body of
the form subscribe and you will be automatically
added to the list. (If you want to get off the list again, send a
message of the form unsubscribe to the same
address.)
There are lots of discussion lists on everything from AA to Zeppelin. If you never get any e-mail, subscribing to a list is a sure way to get some. Some introductory information about E-Mail Discussion Groups is available together with a facility to search for lists that interest you. There is also a list of mailing lists, as well as links at Yahoo to lists and information about how to use the standard LISTSERV and Majordomo interfaces to mailing lists. Many lists have searchable archives, which can be a good source of information.
\parts and
\partslim so that, for
example, \parts{\sin x}{e^x} will produce
output like
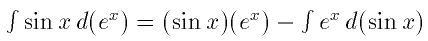
and \partslim{\ln x}{x^2}{2}{3} will produce
output like
.
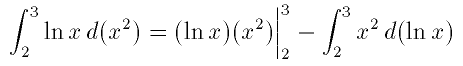(By the way, I did one of those examples in ordinary math mode and the other in display math mode just so you can see the difference; your macros should work in either math mode.) A remark:
\documentclass{article}
\setlength{\textwidth}{4in}
\begin{document}
Here is one fine point about typesetting integrals. Do you see
that $\int x^2 dx$ and $\int x^2 \,dx$ are different? The second
style is preferred. It has a ``thin space'' just before the~$dx$.
You make a thin space via~\verb+\,+ (backslash comma).
\end{document}
intparts command?
Remark: for a lesson plan you may want to make lists. LaTeX has three built-in list structures. For a numbered list, you type:
\begin{enumerate}
\item First item.
\item Second item.
\item And so on.
\end{enumerate}
For a bulleted list, you type:
\begin{itemize}
\item Ho hum.
\item Tra la.
\end{itemize}
For a description or definition list, you type:
\begin{description}
\item[a term] Its definition.
\item[another term] Another definition.
\end{description}
(By the way, there are exact parallels of these structures in
HTML. You type <ol> <li> an item
</ol> for an ordered---that is,
enumerated---list; <ul> <li> an item
</ul> for an unordered---that is,
bulleted---list; and <dl> <dt> a term
<dd> its definition </dl> for a
definition list.)
Last modified and validated: Wed Oct 4 17:32:39 1995