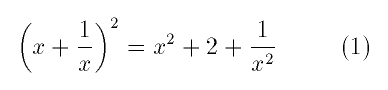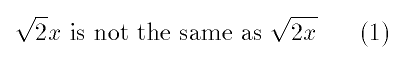Third Class (Wednesday 13 September 1995)
- Learn from experience
- Build a basic World-Wide Web home page
- Increase your fluency with LaTeX
Of course, you may start on the homework during class if you
have time!
- A Maple puzzle.
Take a look at Exercise 12 on page 46 of Chapter 3 of the
CalcLabs with Maple V manual:
A cylindrical can with a top and bottom is
to contain 1000 cubic centimeters. Find
the dimensions of the can if its surface
area is 600 square centimeters.
Note: there are two answers.
Consider the following alleged Maple solution to the problem.
Let r and h denote the radius and the height of
the cylinder. We set up a pair of simultaneous
equations and solve them for r and h.
> eq1:=Pi*r^2*h=1000; eq2:=2*Pi*r^2+2*Pi*r*h=600; fsolve({eq1,eq2},{r,h});
eq1 := Pi*r^2*h = 1000
eq2 := 2*Pi*r^2+2*Pi*r*h = 600
{r = -11.13867027, h = 2.565567417}
Obviously something is wrong here, because it does not make sense
for the radius to be negative!
Write a Maple session, addressed to an audience of first-year
calculus students, that explains the error and exhibits a correct
solution. Turn in hard copy at the next class.
A requirement of this assignment is that your paper include a
Maple plot. (That's also a hint: look at a suitable graph
to see what is going on.) To get a plot into a Maple
worksheet, select "Edit" and "Copy" from the plot window,
move the cursor back into the main Maple window, and
select "Edit" and "Paste".
- Texas A&M University
keeps track of your name, telephone number, e-mail
address, and so forth in an on-line phone book database
named PH. There is an informational page about Locating
People within the Texas A&M University System that
enables you to update your PH
entry. Add your World-Wide Web home-page address to
your PH entry. Your URL (Uniform Resource Locator)
probably has one of the following forms:
- http://calclab.math.tamu.edu/~your-logon-id/
- (if your home page is on the calclab machines)
- /~first-name.last-name/
- (if your home page is on the main mathematics
server)
- http://http.tamu.edu:8000/~your-login-id/
- (if your home page is on tam2000)
- Intelligent mail programs can automatically include a "signature" file
into each mail message you send. (For instance, pine and
emacs have this capability; mailtool, as far as I know, does not.)
Use a text editor to make yourself a signature file. I
change my signature file from time to time; currently it
looks like this:
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Harold P. Boas E-mail: boas@tamu.edu
World-Wide Web URL: /~Harold.Boas/
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Generally, a signature file should contain your name
and some contact information. Some people include little
ASCII pictures or witty sayings. It is recommended that
your signature file not exceed four lines. (If you send
mail from within Netscape, it will complain if your
signature file exceeds four lines, even if some of the
lines are blank.)
Save your signature file as .signature
(that file name starts with
a period.) Then open a terminal window and use the command
chmod a+r .signature to make the file world
readable. Now try sending yourself mail to see if the
signature does get included in your mail message.
I would like to share with all of you some of the ideas,
problems, and errors that I encountered in reading your homework papers.
I enjoyed reading your papers on the subject "Why study
mathematics?" All of them met or exceeded expectations.
I read your papers first of all for content, to see what interesting
ideas you had. Here are some of the common themes mentioned.
- Practical considerations
- Mathematics is needed in everyday life, from such
mundane situations as making change in the grocery
store and understanding mortgage payments to more
sophisticated concerns such as modeling world
population growth and evaluating the data on global
warming.
- Mathematics is fundamental to modern technological
developments that make possible everything from
cordless telephones to CAT scans.
- Studying mathematics can lead to many careers, not
just in scientific disciplines like particle physics and
marine biology, but also in business and industry.
(Of my three college roommates---all mathematics
majors---one became chairman of the statistics
department at a major state university, one works
at Bell Laboratories, and one went to law school
and got a job at a Manhattan law firm. I also know
a PhD mathematician who went on to medical school.)
- Spiritual considerations
- Just as you might go to the recreation center to
exercise your body, studying mathematics exercises
your mind. A good workout makes you feel good.
- If we accept that abstract reasoning is a feature of
our intelligence that distinguishes us from lower
animals, then we can infer that studying
mathematics is a means to developing our full
potential as human beings. Without stretching a
point too much, we could develop this argument to
make the case that studying mathematics is a
religious activity. In this vein, one person
quoted the proverb, "With clarity comes peace of mind."
- Moral considerations. Mathematics, like music, is a
universal language, and learning it is a way to develop
commonalities with people from other cultures. You can
elaborate this point to make an argument for the study of
mathematics as a contribution to world peace.
Secondarily I looked for good style and organization. I would
like to reinforce two points about communicating ideas on paper.
(Three of my four grandparents were English teachers, so good
writing is appreciated in my family.)
- A well-organized essay should have an introduction that
states the thesis, a middle section that develops the
argument, and a concluding section that recapitulates the
theme. The way I learned it in high school, "first you say
what you're going to say, then you say it, and then you
say what you said."
Technical research papers often do not follow this model, but
they probably should. I always start off a research paper
with an introductory section that summarizes the results.
I like to close a research paper with a section on open
problems and directions for future investigations.
- It is often said, with justification, that you should write
from experience. Give concrete examples to support your
points. Instead of writing "mathematics is a foundation
for many careers," write "studying mathematics can lead to
careers in accounting, economics, chemistry, ...." Better
yet, write "Arthur Pancoe, one of the nation's ten best
stockbrokers, attributes his success to the analytical
skills he learned as a mathematics student."
Here are two books I recommend on style.
- William Strunk and E. B. White, The Elements of
Style, third revised edition, New York, Macmillan,
1979. This is also available on computer disk for both Mac
and PC, and on videocassette. It is a classic little book
of advice on good writing.
- Mary-Claire van Leunen, A Handbook for
Scholars, revised edition, New York and Oxford,
Oxford University Press, 1992. This is essential reading
if you are writing a research paper, a dissertation, or a vita.
When I read your papers, I marked errors in grammar, spelling,
punctuation, and so forth. Many of you are not native speakers of
the English language, and I expected you to make some mistakes.
Your grade will not suffer if your English is imperfect, but I
assume that you are interested in improving your English, so I
will continue to correct language errors on your papers.
I always feel embarrassed that I cannot communicate with my
German in-laws in their mother tongue. I hope that those of you
who are foreign-born will not feel embarrassed about your
English. After all, in being able to speak more than one language you are
more capable than many of your fellow students. In this
connection, here are two points to keep in mind.
- I like to tell students that the most successful students
are those who make every possible mistake---once.
- There is a joke that Europeans tell.
- Question: if a person who speaks three
languages is called trilingual, and a person who
speaks two languages is call bilingual, what do you
call a person who speaks only one language?
- Answer: an American.
Those of you who are native speakers of
English---watch out! I have a talent for proofreading.
Finally, I marked errors stemming from improper LaTeX mark-up.
Since this was your first LaTeX paper, I expected you to make
some mistakes in mark-up. If your code was perfect, you exceeded
my expectations. Here is a list of some LaTeX idiosyncrasies that
you should know about.
- Do not use the
" key to make quotation marks in LaTeX.
Instead, make ``smart quotes'' by doubling the ` key for
opening quotes and doubling the ' key for closing quotes.
(Of course, if you are typing in some language other than
English, then quotation marks may have a different
style---but then you probably should be using LaTeX's
babel package that supports multiple languages.)
- In math mode, you can produce primes (derivative symbols)
via
' and ''.
- LaTeX knows how to make accented letters. For example,
\'e produces é and \`a
produces à while \"o produces ö.
- LaTeX normally "stretches" spaces after periods, because it
expects periods to end sentences. Therefore, if a period
follows an abbreviation (but is not the end of a
sentence), you need to alert LaTeX not to stretch the
following space. LaTeX interprets a backslash followed by
a space as an unstretchable space. For example:
Washington Univ.\ is in St.\ Louis. (Don't go
overboard with this. It is not good style to use a lot of abbrevs.)
- You can prevent LaTeX from printing page numbers at the
bottom of the page by putting \pagestyle{empty}
in the preamble of your LaTeX source file. (You might want
to do this for a one-page document, for example.) If you
want to inhibit the page number on a particular page, but
not globally, you can use \thispagestyle{empty}
at the appropriate place in your source file.
- In math mode, you can make a plus-or-minus symbol (as used
in the quadratic formula) with LaTeX's
\pm
control sequence.
- What about parentheses around fractions? You might like the
parentheses to be bigger than usual. You can make LaTeX
adjust the parentheses to the size of the enclosed
subformula by
\left( and
\right). For example:
\begin{equation}
\left(x+\frac1x\right)^2=x^2+2+\frac{1}{x^2}
\end{equation}
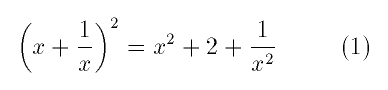
- Remember to use braces
{ and }
for grouping when appropriate.
\documentclass[12pt]{article}
\usepackage{amsmath}
\begin{document}
\begin{equation}
\sqrt2x \text{ is not the same as } \sqrt{2x}
\end{equation}
\end{document}
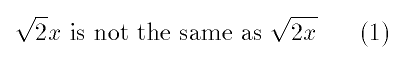
- In revising your Maple worksheets, some of you wanted to
insert a new region before the first line of the
worksheet. You found that "Insert Prompt" on the "Edit"
menu did not work: it made a new line after the first
line. Here is the solution. Put the cursor at the very
beginning of the first line, and then select "Split Region
at Cursor" from the "Edit" menu. That will move the first
line down and make a new line above. You can change the
new region to a text region by putting the cursor there,
clicking the "Input" button, and clicking "Text."
- You get valid, but weird-looking results if you
differentiate a combination of arrow-defined functions by
using the
D operator.
Try converting to Maple expressions and using
diff instead. For example, in exercise 5 on
page 43 of the CalcLabs with Maple V manual,
> f:=x->x^3+3*x+7; g:=x->tan(x^2+1);
3
f := x -> x + 3 x + 7
2
g := x -> tan(x + 1)
you get a strange result if you ask Maple for D(f*g);
(although D(f*g)(x); is fine). What looks better
is diff(f(x)*g(x),x); or
unapply(diff(f(x)*g(x),x),x);
- Here is a little quirk of Maple.
> a:=5; b:=7; f:=x->a*x+b;
a := 5
b := 7
f := x -> a x + b
Why didn't Maple respond f := x -> 5x + 7 instead?
This is another situation in which Maple
behaves better with expressions than with functions. To
get the expected result (as an arrow-defined function), you have to say
f:=unapply(a*x+b,x);
Your first project for the
semester is to build a World-Wide Web home page and to help
someone else build one. The page is supposed to contain at least
one link and one image.
Today we are going to get started by building a simple home page.
During the semester, you will add links and images and further
information to the page, but today the goal is just to get a page
that works.
World-Wide Web pages are written in Hyper Text Mark-up Language
(HTML). This language is similar to LaTeX in spirit. You
prescribe the logical design of the page, but not the
visual design. Thus, you are allowed to say, "This is a
level-three heading," but you are not allowed to say, "This is
centered text in a fourteen point bold sans serif font."
In HTML, most of the mark-up instructions come in grouped
pairs, like LaTeX's \begin{math} ... \end{math} structure. A
typical example of an HTML "tag" is <EM>this is
emphasized text</EM> (emphasized text is typically
displayed in italics, but the font choice is left up to the individual
Web browser). Notice that the start tag is surrounded by angle
brackets, and the end tag looks just the same except that it also
has a slash. It does not matter whether the tags are upper case
or lower case.
Here is a template for a very basic Web page. Use the mouse to
cut this template and paste it into a text editor. Then modify
the information to apply to yourself. Notice that blank lines do
not start new paragraphs, so you can use blank lines to make your
input file more readable. (You must use an explicit
<P> tag to start a new paragraph.)
<html>
<head>
<title>A sample home page</title>
</head>
<body>
<h1>My home page</h1>
<P>
Here is some information about me.
Notice that the paragraph tag P does not need a matching end tag.
<h2>This is a level two header</h2>
<OL>
<LI>This is the first item of an ordered list.
<LI>The list item tag LI is another one that has an optional
end tag.</LI>
</OL>
<h3>Information about me</h3>
<ul>
<li>My e-mail address
<li>My telephone number
<li>And so on; this is an unordered list.
</ul>
</body>
</html>
Here is what will display on the screen:
My home page
Here is some information about me. Notice that the paragraph tag P does not need a matching end tag.
This is a level two header
- This is the first item of an ordered list.
- The list
item tag LI is another one that has an optional end tag.
Information about me
- My e-mail address
- My telephone number
- And so on; this is an unordered list.
After you edit the HTML template, you need to save it as a
file and be sure that Web browsers can find it. Each computer
system has a special location where it expects to find publicly
accessible HTML files. On the calclab machines and the main
mathematics server, the location for HTML files is a subdirectory
named public_html in your home directory; this
subdirectory has probably already been created for you with the
correct access permissions by the system administrator. (On
tam2000, the subdirectory is named .public_html with
an initial period; you will have to create it yourself and make it
world-readable and world-executable.)
Save your basic home page in this special subdirectory with
the name index.html (this is a standard name for home
pages). Use the "Save As" feature on your text editor: you can
probably navigate to the subdirectory public_html
with a mouse click, and then type in the name index.html.
There is one more step: you need to change the access permissions
on index.html to make it a world-readable file. Open
a terminal window, execute the command cd public_html
(on tam2000, cd .public_html)
and then the command chmod a+r index.html.
Now test it out. Open a Web browser (Mosaic or Netscape), click
on the "Open" button, and type in
http://calclab.math.tamu.edu/~your_user_id/ (if your
home page is on the calclab machines) or
/~your_user_id/ (if your home
page is on the main mathematics server) or
http://http.tamu.edu:8000/~your_user_id/ (if your
home page is on tam2000). Your home page should display in the
browser. Now have your neighbor try to display your home page
(this is an extra check to confirm that the file permissions are correct).
When you have time to go further, you can look at some
information for building home pages from the Web Beginner's
Corner at Texas A&M
University, and you can investigate some of the html
resources on our class list of resource
materials.
Other tips:
- There is an automated
validator that will find syntax
errors in your html code.
- If you see a Web page you like, and you are wondering "How
did they do that?", you can examine the html source code by
clicking on "View" and "Source" (in Netscape) or "File" and "View
Source" (in Mosaic).
This exercise was originally planned as homework last week, but
since we ran out of time, it is now part of today's
classwork.
Recall that in the Maple
assignment from last class, you determined a certain third degree
polynomial p.
A little experimentation with Maple will convince you that
p(n) is always an integer when n is an
integer. Find a proof of this fact, write in LaTeX an
explanation suitable for
high school students,
and turn in hard copy by the end of class.
Remark. You can write the polynomial as a fraction whose
numerator is a polynomial q(n) with integral coefficients, and whose
denominator is 6. Hence what you need to show is that the
numerator is divisible by both 2 and 3 (and hence 6) when n is an
integer. If you were writing a solution for a graduate class, you
might (for example) invoke Fermat's little theorem, which says
that a^p is congruent to a modulo p
when a is an integer and p is a prime. For a
high-school audience, however, you need to give a more
elementary, bare-hands presentation.
Finished?
If you have done all the above activities,
and there is still time left, here are some other activities you can do.
- Help someone else.
- Start on the homework.
- Think about the projects.
- Read net news. In Netscape, click on the Newsgroups button.
- Surf the Internet. If you are using Netscape, click on Net
Directory; from Mosaic, click on Navigate and then on
Internet Starting Points.
/ Home / Contents /
Harold P. Boas
Last modified: Sat Jul 30 10:07:18 EDT 2022