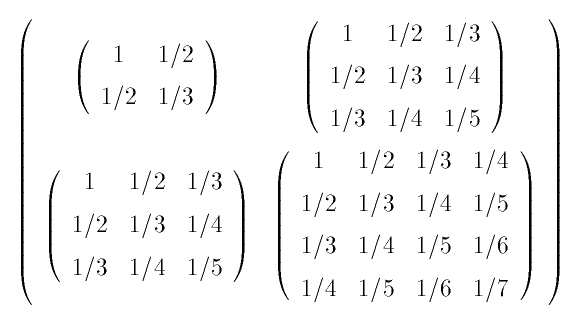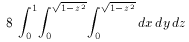
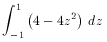
Last time we discussed good style in writing mathematics. Here are some recommended books about writing (mathematics) stylishly.
For the homework problem about finding the volume enclosed by two intersecting cylinders, there were two popular solutions.
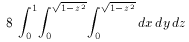
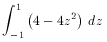
Both methods yield the answer 16/3.
Here are some typical Maple plots to illustrate the problem and to exhibit the squares.
tubeplot({[t,0,0],[0,t,0]}, t=-3..3, radius=1,
tubepoints=20, scaling=constrained);

tubeplot({[t,0,0],[0,t,0]}, t=-3..3, radius=1,
tubepoints=20, scaling=constrained,
style=contour);
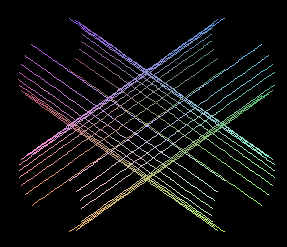
plot3d(min(sqrt(1-x^2),sqrt(1-y^2)), x=-1..1,
y=-1..1, style=contour, shading=ZHUE);
You all know and love systems of simultaneous linear
equations. We have seen that one way to solve linear systems is
via Maple's solve command. For example, if you set
eqns := {u+v+w=1, 3*u+v=3, u-2*v-w=0};
then you can solve(eqns); to get numerical values
for the variables u, v, and w.
Matrices are often an efficient way to handle linear systems. Let's see how Maple deals with matrices.
Open up a Maple session, and load Maple's linear algebra package
via the with(linalg): command. (Do not be concerned
if you get a message from Maple about new definitions for norm
and trace. This message is normal.)
Maple views a matrix as a list of lists. Therefore you can define a matrix with the name A via
A:=matrix( [ [9,13,17], [14,18,22] ] );
Alternatively, you can specify the number of rows and number of columns and give a single list (which Maple will then break up into the appropriate rows). Thus, another way to specify the above matrix is
A:=matrix(2, 3, [9,13,17,14,18,22] );
Still another way to define a matrix is to specify a formula for the entries in terms of the row and column indices. For example, the above matrix can be generated via
A:=matrix(2,3, (i,j)->5*i+4*j);
After you have defined the above matrix A, what happens
if you ask Maple for the value A;? If you want to see the entries
displayed, you must ask Maple for matrix evaluation via
evalm(A);.
Exercise: Use a matrix command to
make Maple display the 4x4 Hilbert matrix whose entry in
the ith row and jth column is
1/(i+j-1). This matrix shows up in numerical analysis,
where it is a standard example of an ill-conditioned matrix. The
Hilbert matrix
is sufficiently common that Maple has a built-in
hilbert command. For comparison with your solution,
try the hilbert(4); command.
Maple knows the standard matrix operations of addition,
subtraction, multiplication, scalar multiplication, forming
inverses, and exponentiation. For the 2x3 matrix A that
you defined above, try evalm(A+A); and
evalm(4*A); for example.
Since A is a 2x3 matrix, it is not possible to multiply
A by itself. Does Maple complain if you ask it for
A^2;? Try it. Now try
evalm(A^2);.
Since Maple uses the asterisk * for scalar
multiplication, Maple needs a different symbol for matrix
multiplication. Maple uses &* for matrix
multiplication.
The above matrix A is a 2x3 matrix, so its transpose is
a 3x2 matrix. Therefore you can multiply A by its transpose
(in either order). Try evalm(A&*transpose(A)); to
evaluate this product. An alternate syntax that computes the same
result is multiply(A, transpose(A));. Do you get the
same answer if you form the product in the other order via
multiply(transpose(A), A);?
Define B:=evalm(A&*transpose(A));. What does Maple
do if you ask for 1/B;? How about
B^(-1);? What about
evalm(1/B);?
You can also use
inverse(B); to display the inverse of a matrix. What
happens if you ask for
inverse(transpose(A)&*A);?
Can you now predict what
det(transpose(A)&*A); will return?
Maple can perform operations on the individual entries of a
matrix. Try map(sin,A); map(evalf,"); for example.
You can also refer to individual entries of a matrix. For
example, A[2,3]; picks out the entry of
A that is in the second row and third column.
Exercise continued: Try the following Maple commands.
Digits:=3; C:=hilbert(4): inverse(map(evalf,C)); inverse(C);
These commands compute (a) the inverse of a three-digit numerical approximation to the Hilbert matrix and (b) the exact inverse of the Hilbert matrix. Do you see any resemblance between the two inverses? Does this explain the terminology "ill-conditioned"?
If Maple can compute it, then LaTeX can typeset it.
The Maple command latex(evalm(A)); will produce the
following LaTeX code. (I have put in some extra carriage returns
for clarity.)
\left[
\begin {array}{ccc}
9&13&17\\
\noalign{\medskip}
14&18&22
\end {array}
\right]
If you put this code inside a LaTeX displaymath
environment, you will get the matrix A typeset. (Since
matrices are large, they are almost always set as displays.)
Here are some points to observe about this code.
\left[ and \right] are
delimiters of adjustable size that make the brackets
around the matrix. If you want parentheses instead of
square brackets, use \left( and
\right). To make vertical bars for
determinants, use \left\vert and
\right\vert. You can also make curly braces via
\left\{ and \right\}. (For curly
braces, you need to put a backslash in front of the braces
so that LaTeX realizes they are not LaTeX grouping symbols.)
array environment has an argument,
in this case ccc, that determines how the
entries in each column are aligned. In this example, all
entries are centered in their columns. If you change
ccc to lrc, for example, then
the entries in the first column will be left-aligned, the
entries in the second column will be right-aligned, and
the entries in the third column will be centered.
& character is used to separate entries
in different columns.
\\ is used to terminate
each row of the matrix except the last one.
\noalign{\medskip} in this example is an
extra space between the rows of the matrix. This extra
space is not necessary and could be deleted.
(If you \usepackage{amsmath}, and you are willing to
settle for centered entries in matrices, then you can replace
the array environment with the matrix
environment, which does better spacing. The amsmath
package also has a pmatrix environment that has
enclosing parentheses built in.)
Exercise: Typeset the following matrix. Hint: make Maple do (most of) the work. The (i,j) entry of the matrix is the anti-derivative of the fraction (x^2+i)/(x^2+j).
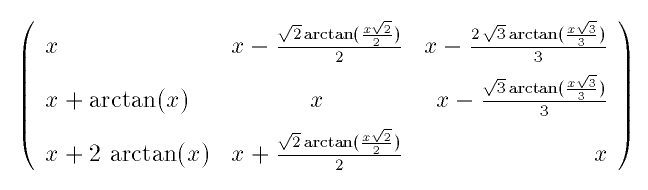
As an application of matrices, let's implement a simple cipher. In doing this, we will also see an example of a simple Maple program.
At this point, it would be a good idea to reinitialize your Maple
session.
(On the File menu, click on New. Then load
with(linalg): again.) We are going to be using the
alphabetic characters as names for themselves, so if you have
A and B defined as matrices, it may cause problems.
The idea behind the cipher is first to translate letters into numbers via A->1, B->2, and so on. After translating a message into a string of numbers, encode the message in the following way. Break the string of numbers into blocks of five, view these blocks as the rows of a matrix, and multiply this matrix on the right by a specified 5x5 matrix. This renders the message unintelligible. However, if the recipient of the message knows the matrix (and hence the inverse matrix), then the recipient can recover the original plain text.
To make the procedure a little more sophisticated, we will do the arithmetic modulo 59.
Here is the 5x5 matrix we will use.
[ 47 41 31 33 56 ]
[ ]
[ 1 12 27 12 57 ]
[ ]
[ 41 1 28 53 58 ]
[ ]
[ 35 24 32 23 34 ]
[ ]
[ 19 9 29 6 26 ]
I generated this random matrix via map(x->modp(x,59),
randmatrix(5,5));.
You can cut and paste the definition of the matrix into Maple via
Mtrx:=matrix([[47,41,31,33,56],[1,12,27,12,57], [41,1,28,53,58],[35,24,32,23,34],[19,9,29,6,26]]);
(I generated this list format for the matrix via
convert(",listlist);.)
Your task is to follow the hints to decode this message:
[ 10 54 21 45 52 ]
[ ]
[ 52 3 57 6 38 ]
[ ]
[ 52 8 8 39 56 ]
[ ]
[ 17 9 56 35 10 ]
[ ]
[ 5 27 53 1 23 ]
[ ]
[ 45 17 20 6 27 ]
[ ]
[ 11 19 27 29 6 ]
[ ]
[ 49 35 38 19 43 ]
[ ]
[ 10 50 2 6 23 ]
[ ]
[ 21 11 52 32 4 ]
[ ]
[ 53 21 9 50 43 ]
[ ]
[ 5 27 53 1 23 ]
[ ]
[ 36 41 41 49 11 ]
[ ]
[ 17 25 47 25 18 ]
[ ]
[ 49 40 46 19 4 ]
[ ]
[ 42 53 22 3 57 ]
[ ]
[ 48 18 7 9 38 ]
[ ]
[ 29 34 45 0 58 ]
[ ]
[ 13 46 27 46 17 ]
[ ]
[ 52 13 55 35 45 ]
[ ]
[ 30 44 4 42 15 ]
To get this message into your Maple session, cut and paste
Secret:=matrix([[10,54,21,45,52],[52,3,57,6,38], [52,8,8,39,56],[17,9,56,35,10], [5,27,53,1,23],[45,17,20,6,27], [11,19,27,29,6],[49,35,38,19,43], [10,50,2,6,23],[21,11,52,32,4], [53,21,9,50,43],[5,27,53,1,23], [36,41,41,49,11],[17,25,47,25,18], [49,40,46,19,4],[42,53,22,3,57], [48,18,7,9,38],[29,34,45,0,58], [13,46,27,46,17],[52,13,55,35,45], [30,44,4,42,15]]);
To create the secret message, I first defined a list of the alphabetic characters. This requires a little care. First of all, Maple thinks that I represents the square root of minus one, so I had to undo this convention by aliasing I to itself. Also, I gave punctuation characters symbolic names to avoid confusion (since Maple uses some punctuation characters for special purposes). Here are my definitions, which you will need to copy into your Maple session.
space:=` `: period:=`.`: comma:=`,`: semicolon:=`;`: colon:=`:`: bang:=`!`: query:=`?`: alias(I=I); Alphabet:=[A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R, S,T,U,V,W,X,Y,Z,a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p, q,r,s,t,u,v,w,x,y,z,space,period,comma, semicolon,colon,bang,query];
Now if you ask Maple for Alphabet[28]; for example,
you should get the 28th element of the list Alphabet, which
is the lower case letter b.
To convert numbers into letters, define a function
NumToAlph as follows.
NumToAlph:=n->Alphabet[ modp(n-1,59) +1 ];
The reason for adding and subtracting 1 in this definition is that
modp returns values between 0 and 58, while the
index parameter for
the list Alphabet runs from 1 to 59.
Test this definition by checking NumToAlph(5); and
NumToAlph(50); for example.
You can define an inverse function AlphToNum that
converts letters into
numbers by executing the following do loop.
for counter from 1 to 59 do AlphToNum(Alphabet[counter]):=counter: od:
Notice that there is no semicolon after the do.
(Usually one writes a do loop in the form for
i from 1 to n do, but in this example single letters are
reserved as names of alphabetic characters, so I named the
counter in the loop "counter" instead of "i".)
Try AlphToNum(a); and AlphToNum(` `);
to confirm that the function is defined correctly.
If you have a message written as a list of alphabetic
characters, you can convert it into a list of numbers via
map(AlphToNum,CharacterList);. Try converting the list
[H,e,l,l,o,space,w,o,r,l,d] for example.
Conversely, if you have a list of numbers, you can convert it
to a list of letters via map(NumToAlph,NumberList);.
Try converting the list
[22, 31, 44, 51, 53, 33, 41, 41, 30, 58] for example.
You should get a list of letters inside square brackets.
To convert this list into words,
try cat(op[1](")); to concatenate the
letters in the list.
Now see if you can decode the secret message. You need to
multiply the message on the right by the inverse of the matrix
Mtrx and then convert back to alphabetic characters.
Exercise: Use Mtrx to encode your
own message. Send the message by e-mail to your neighbor for
decoding.
Tip: One problem I had to solve before converting my secret message into numeric form was how to change a string of characters into a comma-separated list. (Of course, I could have typed in all the commas, but that would have been tedious.) I wrote the following little Maple procedure. (Maple programs are called procedures. Chapter 13 of the CalcLabs with Maple V manual is an introduction to programming with Maple.)
MessageToList:=proc(Message)
local cntr,MessageList;
MessageList := NULL;
for cntr to length(Message) do
MessageList := MessageList,substring(Message,cntr .. cntr);
od;
MessageList := [MessageList];
end;
Here is a line-by-line explanation of this procedure.
MessageToList:=proc(Message)
MessageToList. The proc is a
Maple keyword that indicates the beginning of a procedure (a
program). This procedure defines a function that has one
argument, which is named Message. Here
Message acts as a dummy variable.
local cntr,MessageList;
cntr is going to be a counter for a loop, and
the variable MessageList is going to hold the
comma-separated list.
MessageList := NULL;
MessageList to
be an empty string.
for cntr to length(Message) do
do. By default, the counter
cntr starts at 1, and it is
incremented by one unit each time through the loop. The
loop terminates when the counter reaches the length of the
string Message (the string that is the input
to the procedure).
MessageList := MessageList,substring(Message,cntr .. cntr);
substring function picks out of
Message the part starting at the position of
the counter and ending at the position of the counter. In
other words, it picks out a single character at the
position of the counter. Then MessageList is
replaced by itself with this character appended following
a comma.
od;
do backwards: it signals the
end of the statements that are included in the
do loop.
MessageList := [MessageList];
MessageList to be itself
enclosed in brackets, so that it is now a Maple list
structure. This list is the output of the procedure.
end;
In summary,
this procedure takes one argument Message and runs a
loop that picks out each one-character substring at position
cntr and appends it to a comma-separated list. The
procedure returns that list. The procedure uses two local
variables: cntr is the counter for the loop, and
MessageList holds the current value of the
comma-separated list of characters.
Now executing the Maple command
MessageToList(`Take but degree away, untune that string, And hark! what discord follows; each thing meets In mere oppugnancy. Troilus and Cressida, Act I, scene iii.`);
produces the output
[T, a, k, e, , b, u, t, , d, e, g, r, e, e, , a,
w, a, y, ,, , u, n, t, u, n, e, , t, h, a, t,
, s, t, r, i, n, g, ,, , A, n, d, , h, a, r,
k, !, , w, h, a, t, , d, i, s, c, o, r, d, ,
f, o, l, l, o, w, s, ;, , e, a, c, h, , t, h,
i, n, g, , m, e, e, t, s, , I, n, , m, e, r,
e, , o, p, p, u, g, n, a, n, c, y, ., , T, r,
o, i, l, u, s, , a, n, d, , C, r, e, s, s, i,
d, a, ,, , A, c, t, , I, ,, , s, c, e, n, e,
, i, i, i, .]
Notice the backquotes ` that I used to convert the poetry into a
Maple string. If you cut and paste the poem into Maple, be careful
not to introduce newline characters into the string, or Maple
will complain.
gausselim that performs Gaussian elimination
to take a matrix to row echelon
(upper triangular) form. Maple also has a command
gaussjord that takes a matrix to reduced row
echelon form. For example, try
A:=matrix(3,4,max); and then either
gausselim(A); or gaussjord(A);.
addrow, mulrow, and
swaprow commands to do the steps of
Gauss-Jordan elimination one at a time. It also knows how
to augment a matrix. This can be useful for
preparing examples for a class.
array environments. Typeset the
following matrix. Hint: Maple can assist you; the
submatrices are Hilbert matrices.