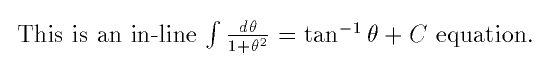
Here is some information about how to use LaTeX. These instructions are part of the course Mathematical Communcation and Technology in the Department of Mathematics at Texas A&M University.
To use LaTeX happily, you need to understand its design philosophy.
Your main concern in writing a document should be the content, not the form. Pay attention to what you want to convey to the reader, pay attention to organization, pay attention to clarity of exposition; but don't worry a lot about the fine points of the appearance of the printed output.
If you let LaTeX do its job, it will make
pretty good decisions about spacing, line and page breaks, page
numbering, and so forth. While you are writing, you should not
be trying to tell LaTeX "make this heading centered fifteen point
bold italic"; instead, you should tell LaTeX to start a
\subsection, and let LaTeX choose the font and
style.
Designing the visual appearance of a document is a hard job to do well. Someday you are going to want to override LaTeX's default design (maybe you have to submit to the whims of the thesis clerk), but don't worry about this at the beginning. Concentrate on what you want to say.
Here is what Leslie Lamport (creator of LaTeX) says on this subject in section 1.4 of his user's guide:
The primary function of almost all the LaTeX commands that you type should be to describe the logical structure of your document. As you are writing your document, you should be concerned with its logical structure, not its visual appearance. The LaTeX approach to typsetting can therefore be characterized as logical design.
LaTeX is a mark-up language as opposed to a WYSIWYG (what you see is what you get) system. This is in accordance with LaTeX's logical design philosophy as opposed to visual design.
Suppose, for example, that your thesis advisor orders you to
change all the theorem statements in your dissertation from
italic to boldface. With a WYSIWYG system, you would have to
change each theorem by hand. With LaTeX's logical design, all you
would do is to redefine the theorem environment in
the preamble of your LaTeX input file.
Or suppose you have to typeset a big hairy formula 56 times. In
LaTeX, you would say \newcommand{\bighairyformula}{some
complicated ... math commands} to define a new control
sequence, and then you would just type
\bighairyformula 56 times. Now when your picky
coauthor insists that the Greek rho in the formula should really
be a Greek sigma, you just change the definition of
\bighairyformula. You don't have to edit 56
formulas, the way you would with a WYSIWYG system.
There are instructions for running LaTeX in the second class.
Equations come in two flavors: short in-line equations that do not interrupt the paragraph, and displayed equations that are printed on a separate line. All mathematics formulas are enclosed between special delimiters that signal LaTeX to switch to its special mathematics mode.
For example, here are three equivalent ways to write the same anti-derivative formula from calculus as an in-line equation.
This is an in-line $\int
\frac{d\theta}{1+\theta^2} = \tan^{-1}\theta+C$ equation.
This is an in-line \(\int\frac{d\theta} {1+\theta^2}=
\tan^{-1} \theta+C\) equation.
\(
and \) pair.
This is an in-line \begin{math}\int\frac {d\theta}{1+\theta^2}
= \tan^{-1} \theta+ C\end{math} equation.
\begin{math} and \end{math} pair.
Here is the output as formatted by LaTeX:
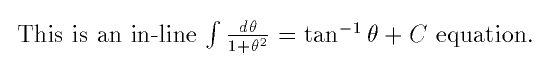
Here are a few points to note about this example.
\sin, \cos, and so on
give the trigonometric functions; \int makes
an integral sign; \frac builds a fraction
whose numerator and denominator are the subsequent two
items enclosed in curly braces.
\gamma
produces a gamma, and \Gamma produces a
capital gamma.
\{
in your input file.)
^ makes a superscript, and an underscore
_ makes a subscript.
To format the same formula as a displayed equation that stands on its own line, just change the delimiters. Each of the following produces a displayed equation.
Here is a displayed \[\int\frac{d\theta}
{1+\theta^2}= \tan^{-1}\theta+C\] equation.
\[ and \] pair delimit
display math mode.
Here is a displayed \begin{displaymath}\int\frac {d\theta}{1+\theta^2} =\tan^{-1}
\theta+ C\end{displaymath} equation.
Here is a displayed \begin{equation}\int
\frac{d\theta}{1+\theta^2}=\tan^{-1}\theta+C\end{equation}
equation.
displaymath
environment and the equation environment: the latter
automatically typesets a formula number.
The formatted output looks like this:
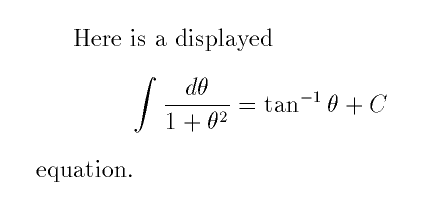
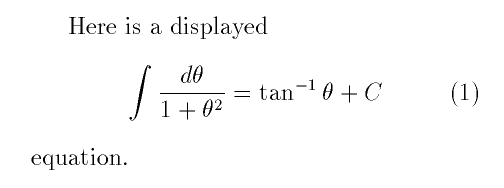
Warning to former plain TeX users: in plain TeX, double
dollar signs $$ are used to delimit display math,
but this convention does not work properly in LaTeX.
Do not use it!
It is a convenient feature of LaTeX that it can automatically generate formula numbers. If you add or delete a numbered equation, you do not have to worry about revising the formula numbers: LaTeX does this chore for you.
What if you want to refer to a numbered equation by number? How
do you manage this if the equation number is automatically
generated? LaTeX has a simple \label and
\ref mechanism for handling symbolic cross
references. Here is an example.
The formula \begin{equation} E=m c^2
\label{Einstein} \end{equation} has passed into popular culture,
but the true significance of the mass-energy
equation~(\ref{Einstein}) is~\ldots
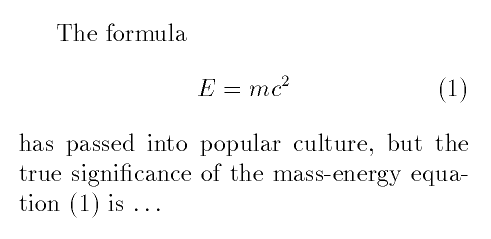
(By the way, that tilde ~ is a
tie or non-breaking space: it is good type-setting style to keep a
short label attached to its noun.)
If you use the amsmath package described below, then you can type
\eqref instead of \ref, and the
parentheses around the cited equation number will be supplied
automatically.
If you are going beyond the most basic level of displayed equations, I recommend that you use the amsmath package that plugs into LaTeX. This has lots of useful features for multi-line equations, compound symbols, even commutative diagrams!
To load this
package, put the command \usepackage{amsmath} in the
preamble of your LaTeX input file. Now you can make aligned
equations, for example, like this:
\documentclass[12pt]{article}
\usepackage{amsmath}
\begin{document}
\begin{align}
\cos^2\psi+\sin^2\psi & = 1, \\ \cosh^2\omega-\sinh^2\omega &=1.
\end{align}
\end{document}
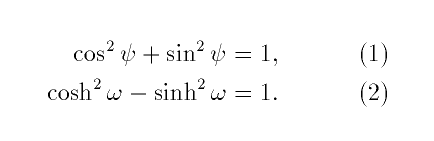
Here the separate
lines of the display are separated in the input file
by a double backslash \\, and
the alignment point(s) are indicated by ampersands
&. Notice the automatically generated equation
numbers; you can suppress the equation numbers via
\begin{align*} ... \end{align*} (the "star form" of
the align environment).
The amsmath package was created by the American Mathematical Society and some of the gurus of the LaTeX3 project to augment LaTeX's mathematics capabilities. It is related to, but not the same as, the AMS-TeX macro package that supplements plain TeX. For further information about the amsmath package, you can view the AMS-LaTeX user's guide as a dvi file (looks better on the screen) or as a PostScript file (can be sent to the printer for hard copy). This user's guide is incorporated into Chapter 8 of the LaTeX Companion.