Record of daily activities and homework, Math
409-502, Advanced Calculus I, Fall 2004
- Monday, August 30
- We discussed the fundamental completeness property of the real
numbers stating that a bounded monotonic sequence has a limit, and
we looked at some examples of sequences of real numbers.
Homework for Wednesday:
- Read Chapter 1 in the textbook (pages 1-12).
- Group number n should be prepared to present in class the
Exercises for section 1.(n+1) on pages 12-13.
- Wednesday, September 1
- We looked at solutions to some of the Exercises for
Chapter 1.
Homework for Friday:
- Read Chapter 2.
- Do Exercise 2.3/1 on page 31 (to hand in).
- Friday, September 3
- We discussed various notions from Chapter 2: working with
inequalities and absolute value, estimating size, finding upper and
lower bounds, and proving boundedness or unboundedness of
sequences.
Homework for Monday:
- Read section 3.1, pages 35-38.
- Do Exercise 2.6/3 on page 32 and Exercise 3.1/1(b) on
page 46 (to hand in on Monday).
In doing these exercises, you may find it useful to consult
Question 2.6/3 on page 30 and its answer on page 34,
and Question 3.1/1 on page 38 and its answer on
page 49.
- Monday, September 6
- We looked at examples of proving existence of limits (including
infinite limits).
Homework for Wednesday:
- Read sections 3.2-3.5, pages 38-43.
- Do Exercises 3.1/2 and 3.3/1(a) on pages 46-47.
- Wednesday, September 8
- We worked on Exercises 3.4/1-5 on page 47 concerning
limits related to the limit of an as n tends to
infinity.
Homework for Wednesday:
- Read sections 3.6-3.7 (pages 44-45) and 4.1
(page 51).
- Do Problem 2-1 on page 32.
- Friday, September 10
- We discussed limits of some special sequences, such as
nan and a1/n.
Homework for Monday:
- Read the rest of Chapter 4 (pages 52-57).
- Do Problem 4-1 on page 59: namely, prove using the
definition of limit that n1/n→1 as
n→∞.
- Monday, September 13
- We discussed various methods for proving the existence of
limits, and we worked an example showing that the limit of
integrals is not necessarily equal to the integral of the limit.
The slides from the lecture are
available.
Homework for Wednesday:
- Do Exercise 3.6/1 on page 47 and Exercise 4.4/1
on page 58.
- Read section 5.1, pages 61-64.
- Wednesday, September 15
- We discussed the homework problems and the squeeze theorem for
limits.
Homework for Friday:
- Finish the homework from last time.
- Read sections 5.2 and 5.3, pages 64-68.
- Do Exercise 5.1/1 on page 73.
- Friday, September 17
- We reviewed limit theorems for sequences and discussed the
notion of subsequence. The slides from the lecture are available.
Homework for Monday:
- Read sections 5.4 and 5.5, pages 68-73.
- Do Problem 5-7, page 75.
- Monday, September 20
- We discussed the nested interval theorem, the
Bolzano-Weierstrass theorem, and the notion of cluster point. The
slides from the lecture are
available.
Homework for Wednesday:
- Read sections 6.1-6.3, pages 78-83.
- Do Exercises 6.2/1 and 6.3/1 on pages 89-90.
- Wednesday, September 22
- We discussed Cauchy's criterion for convergence and the notions
of supremum, infimum, limsup, and liminf.
Homework for Friday:
- Read sections 6.4-6.5, pages 83-89.
- Do Exercises 6.4/3 and 6.5/1 on page 90.
- Friday, September 24
- We discussed a comparison test for convergence of infinite
series and looked at examples.
Homework for Monday:
- Read sections 7.1 and 7.2, pages 94-100.
- Do Exercise 7.2/2 on page 109 and Problem 5-5 on
page 75.
- Monday, September 27
- We discussed convergence tests for infinite series, including
the root test. The slides from the lecture are
available.
Homework for Wednesday:
- Read sections 7.3 and 7.4, pages 100-104.
- In preparation for the examination, make a list of the main
definitions and theorems in the course so far.
- Wednesday, September 29
- We reviewed for the examination to be given on Friday.
Homework for Friday: Study for the exam.
- Friday, October 1
- First examination
- Monday, October 4
- The graded examinations were returned, and we discussed the
asymptotic comparison test and the integral test for convergence of
infinite series.
Homework for Wednesday:
- Read sections 7.5-7.7, pages 104-109.
- Do Exercises 7.4-7.5/1a,b,c on page 110 and 7.7/1 on
page 111.
- Wednesday, October 6
- We reviewed convergence tests for infinite series, discussed
Cauchy's condensation test (which is not in the textbook), and
began a discussion of convergence of power series. The slides from
the lecture are available.
Homework for Friday:
- Read section 8.1, pages 114-117.
- Do Exercise 7.6/1a,c on page 111.
- Do Exercise 8.1/1g on page 123.
- Friday, October 8
- We worked on some exercises about convergence of power series
(Exercise 8.1/1 on page 123).
Homework for Monday:
- Read sections 8.2, 8.3, and 8.4 (pages 117-122).
- Do Exercise 8.3/1 on page 123.
- Do Problem 7-2 on page 111 (assume that an
and bn are non-zero for all n).
- Monday, October 11
- We discussed endpoint convergence of power series and the
multiplication theorem for absolutely convergent series (including
a counterexample for conditionally convergent series that is not in
the book). The slides from the lecture are
available.
Homework for Wednesday:
- Read Chapter 9, pages 125-134.
- Do Exercises 9.2/3 and 9.3/1, pages 134-135.
- Wednesday, October 13
- We discussed some of the homework problems and considered group
structures on sets of functions. The slides from the lecture
are available.
Homework for Friday:
- Read sections 10.1 and 10.2, pages 137-142.
- Do Exercises 10.1/2 and 10.2/1 on page 148.
- Friday, October 15
- We discussed approximation of functions and the contrast
between local properties of functions and global properties of
functions.
Homework for Monday:
- Read sections 10.3 and 10.4, pages 143-147.
- Do Exercise 10.3/2 on page 149.
- Do Problem 10-2 on page 150.
- Monday, October 18
- We discussed the notions of limits of functions and continuity
of functions. The slides from the lecture are
available.
Homework for Wednesday:
- Read sections 11.1 and 11.2, pages 151-158.
- Do Exercises 11.1/5 and 11.2/1 on page 167.
- Wednesday, October 20
- We continued the discussion of limits and continuity, and we
worked in groups on some problems about limits. The slides from the
lecture are available.
Homework for Friday:
- Read sections 11.3, 11.4, and 11.5, pages 158-167.
- Do exercises 11.4/1 and 11.5/1 on page 168.
- Friday, October 22
- We discussed the theorem that a continuous function on a
compact interval has a range that is again a compact interval. The
slides from the lecture are
available.
Homework for Monday:
- Read sections 12.1 and 12.2, pages 172-177.
- Do Exercises 12.1/1 and 12.1/5 on page 180.
- Monday, October 25
- We discussed continuity, the intermediate-value property,
monotonicity, the existence of inverse functions, and relations
among these properties. The slides from the lecture are available.
Homework for Wednesday:
- Read sections 12.3 and 12.4 (pages 178-180) and sections 13.1
and 13.2 (pages 185-187).
- Do Exercise 12.4/2 on page 181 and Exercise 13.1/1a,b
on page 192.
- Wednesday, October 27
- We discussed two properties of continuous functions on compact
intervals: boundedness and existence of extreme values. The slides
from the lecture are available.
Homework for Friday:
- Read sections 13.3 and 13.4, pages 187-190.
- In preparation for the examination, make a list of the main
definitions, concepts, and theorems from sections 7.5 through
13.4.
- Friday, October 29
- We reviewed for the examination and discussed some homework
problems. The slides from the lecture are
available.
Homework for Monday: Study for the
examination.
- Monday, November 1
- Second examination
- Wednesday, November 3
- The graded examinations were returned, and we discussed some of
the problems. The slides from the lecture are
available.
Homework for Friday: Use the ε-δ
definition of continuity to prove that
- the function 1/x2 is continuous at the
point 1;
- the function 1/x is continuous at the point 1/10.
- Friday, November 5
- We discussed uniform continuity and the theorem that a
continuous function on a compact interval is uniformly continuous.
The slides from the lecture are
available.
Homework for Monday:
- Read section 13.5, pages 190-192.
- The interval [0,∞) is not compact. Show nonetheless that
the function √x is uniformly continuous on this unbounded
interval.
- The interval (0,1) is not compact. Determine (with proof)
whether sin(1/x) is uniformly continuous on this open
interval.
- Monday, November 8
- We discussed the definition of the derivative and the
mean-value theorem. The slides from the lecture are available.
Homework for Wednesday:
- Read Chapter 14 (pages 196-204) and section 15.1 (pages
210-211).
- Do Exercise 14.1/3 on page 205.
- Do Exercise 15.1/4 on page 218.
- Wednesday, November 10
- We discussed Cauchy's mean-value theorem and l'Hôpital's
rule. The slides from the lecture are
available.
Homework for Friday:
- Read sections 15.2-15.4, pages 212-217.
- Do Exercise 14.3/2 on page 206.
- Do Exercise 15.4/2 on page 219.
- Friday, November 12
- We discussed Taylor's formula. The slides from the lecture
are available.
Homework for Monday:
- Read sections 17.1-17.3, pages 231-236.
- Suppose you were to plot the functions y=cos(x) and
y=1-x2/2 on the same graph with the x and y axes
scaled in inches (1 inch = 1 radian) using a line
thickness of 1 point (where 1 inch =
72 points).
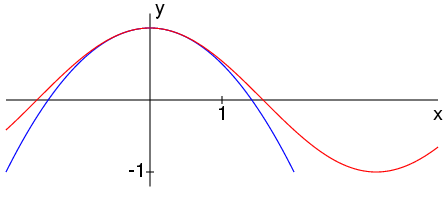
Over what interval of the x-axis would the two curves be
indistinguishable? Why?
- Monday, November 15
- We discussed Taylor's theorem, Taylor series, and analytic
functions. The slides from the lecture are
available.
Homework for Wednesday:
- Read section 17.4, pages 236-238.
- The third examination is scheduled for Wednesday,
December 1.
One of the problems on the exam will be to prove a version of
l'Hôpital's rule selected from the following eight
possibilities: {0/0 or ∞/∞} and {x→a or
x→∞} and {lim f'(x)/g'(x)=L or lim
f'(x)/g'(x)=∞}.
Work on proofs of two cases (to discuss in class).
The method of dividing the cases that I suggested in class does not
work. Here is a new scheme:
- Cases (x→a, 0/0, f'(x)/g'(x)→L) and (x→∞,
∞/∞, f'(x)/g'(x)→∞)
- Cases (x→a, 0/0, f'(x)/g'(x)→∞) and
(x→∞, ∞/∞, f'(x)/g'(x)→L)
- Cases (x→a, ∞/∞, f'(x)/g'(x)→L) and
(x→∞, 0/0, f'(x)/g'(x)→∞)
- Cases (x→a, ∞/∞, f'(x)/g'(x)→∞) and
(x→∞, 0/0, f'(x)/g'(x)→L)
- Wednesday, November 17
- We discussed the notion of (Riemann) integrability. The slides
from the lecture are available.
Homework for Friday:
- Read sections 18.1 and 18.2, pages 241-244.
- Consider the integrable function f(x)=x on the interval [1,2].
How small must the mesh of a partition be in order to guarantee
that the upper sum and the lower sum differ by less than 1/10?
- Do exercise 18.2/3 on page 248.
- Friday, November 19
- We proved that monotonic functions are integrable and that
continuous functions are integrable. The slides from the lecture
are available.
Homework for Monday:
- Read sections 18.3 and 18.4, pages 244-248.
- Prove that if a function f is defined and bounded on [a,b]
and is continuous except at one point, then f is
integrable.
- Do exercise 18.4/2 on page 249.
- Monday, November 22
- We discussed Riemann sums and the fundamental theorem of
calculus. The slides from the lecture are
available.
Homework for Wednesday:
- Read sections 19.1-19.3, pages 251-256.
- Work on proving various versions of l'Hôpital's
rule.
A sketch of one case is at the end of today's slides.
- Wednesday, November 24
- We worked on proofs of l'Hôpital's rule.
- Monday, November 29
- We reviewed for the examination to be given on Wednesday, and
we discussed the second part of the fundamental theorem of
calculus.
Homework for Wednesday: study for the
examination.
- Wednesday, December 1
- Third examination
- Friday, December 3
- We discussed uniform convergence and three theorems about
uniform convergence. The slides from the lecture are available.
Homework for Monday: Read sections 22.1-22.5,
pages 305-318.
- Monday, December 6
- We looked at some additional examples related to uniform
convergence. The slides from the lecture are
available.
Reminder: the final examination is scheduled for
Tuesday, December 14, 8:00-10:00 am.
- Tuesday, December 14
- Final examination
